







The Wave Matrix
A sinusoidal wave traveling along a string looks quite different from a light ray, but the same variables, displacement and slope, can be used to describe it as it passes a reference plane. In geometrical optics the slope was expressed as an angle, and all angles were assumed to be small enough for the sine and tangent of an angle to equal the angle in radians. For a wave on a string, the slope is taken to be the derivative of the displacement with respect z (if the z-axis is the direction of propagation), and no small-angle approximation is made. (For an electromagnetic or quantum-mechanical wave, the concept of angle does not even enter because the quantity involved is not a displacement.) We will use y and y' as the variables to describe a wave, with the prime standing for differentiation with respect to z. We will see that we need only one wave propagation matrix, the translation matrix relating y and y' at reference planes separated by a distance d. This matrix can be found using a little trigonometry:
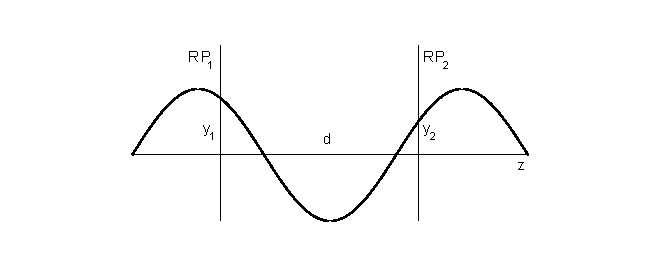
Fig.1 Harmonic wavetrain passing reference planes a distance d apart.
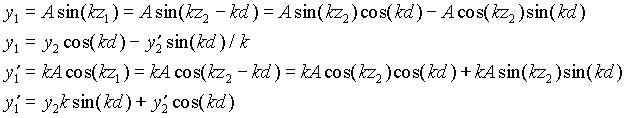
Written as a matrix equation,
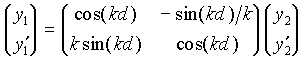 (1)
(1)
In the equations, k has its usual meaning, 2p/l , and note that no assumption is made about the direction of propagation.
The reason that we do not need an interface matrix analogous to the refraction matrix in geometrical optics is that y and y' are continuous across boundaries. This is required by Newton's law for mechanical waves, by Maxwell's equations for optical waves, and by the Schrodinger equation for quantum-mechanical waves.
Eq.1 is used in a different manner in wave optics from the way matrices are used in geometrical optics. When a wave strikes a surface, two waves are produced: a transmitted wave and a reflected wave. Eq.1 relates the transmitted wave to the superposition of the incident and the reflected waves. We can specify the incident wave, but we have to find the reflected wave. The problem is to solve the two linear equations for two unknowns: the amplitudes of the reflected and transmitted waves. (Phase can be dealt with by making the unknowns complex.)
The easiest way to do the algebra is to use complex exponentials to describe the waves. (In the case of quantum mechanics this is more than a convenience: the waves are inherently complex.) A typical situation is illustrated in the figure:
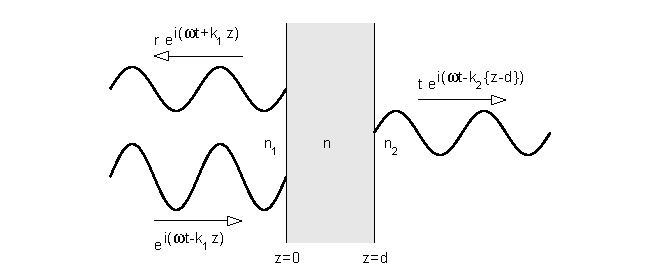
Fig.2 A wave of unit amplitude incident from a
medium of index n1
on a substrate of index n2 covered by a film of index
n.
A wave of unit amplitude is incident from the left on the surface of the film and a wave of amplitude r is reflected. A wave of amplitude t is transmitted into the substrate. Note that the z-axis origin is placed at the film surface, and that the symbol t is used both for time and for the transmitted amplitude. Time is eliminated from the equation when the common factor exp(iwt) is cancelled, and Eq.1 becomes:
![]() (2a)
(2a)
The equation can be simplified by noting that k is 2p n/l 0, and the common factor can be cancelled except in the product kd for which the symbol b will be used
![]()
In addition, a number of minus signs can be eliminated by bringing the i's into the matrix, and writing the equation
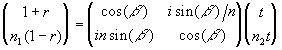 (2b)
(2b)
The two forms of Eq.2 are completely equivalent. Either can be solved for the complex numbers r and t that give the amplitude and phase of the reflected and transmitted waves. Although the computation involves nothing more than straightforward algebra, it can be tedious unless one is using a calculator (such as an HP48) or a computer language that deals directly with complex numbers. We give examples of the solution of Eq.2 in the next three sections.