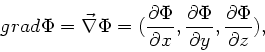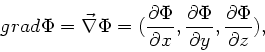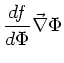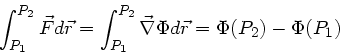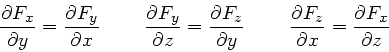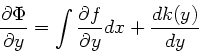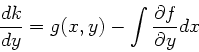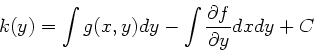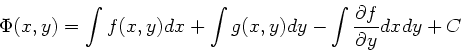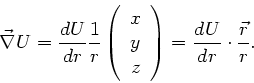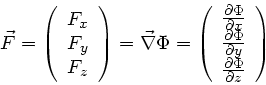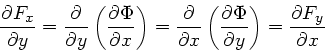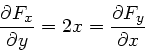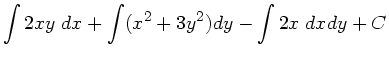Rechenübung am 4. November 1999
Der Gradient und die Existenz von Potentialen.
In der Vorlesung wurde der Begriff des Gradienten eingeführt. Die
Definition ist:
wobei 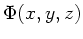 eine skalare Funktion ist. Die wichtigsten
Rechenregeln sind:
eine skalare Funktion ist. Die wichtigsten
Rechenregeln sind:
Diese Regeln sind ähnlich den bekannten Differentiationsregeln von
Funktionen mit einer Veränderlichen.
Aufgabe 1: Sei 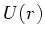 eine nur vom Radius
eine nur vom Radius
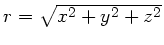 abhängige
Funktion. Zeigen Sie, daß dann gilt:
abhängige
Funktion. Zeigen Sie, daß dann gilt:
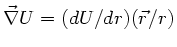 .
.
In der Vorlesung wurde diskutiert, daß bei einer konservativen Kraft
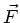 die Arbeit, die benötigt wird um von einem Punkt
die Arbeit, die benötigt wird um von einem Punkt  zu
einem anderen Punkt
zu
einem anderen Punkt 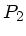 zu gelangen, nicht vom dem Weg abhängt,
der die beiden Punkte verbindet. Falls man auf zwei Integrationswegen
zu verschiedenen Ergebnissen für die Arbeit kommt, hat man es sicher
mit einer nicht konservativen Kraft zu tun und es existiert kein
Potential. Die Umkehrung ist dagegen nicht so einfach. Man kann durchaus
auf zwei bestimmten Wegen zum gleichen Ergebnis kommen, trotzdem muß
die Kraft nicht konservativ sein. Die Bedingung ist eben gerade,
daß man auf allen Wegen zum gleichen Ergebnis kommt.
Falls allerdings eine skalare Funktion
zu gelangen, nicht vom dem Weg abhängt,
der die beiden Punkte verbindet. Falls man auf zwei Integrationswegen
zu verschiedenen Ergebnissen für die Arbeit kommt, hat man es sicher
mit einer nicht konservativen Kraft zu tun und es existiert kein
Potential. Die Umkehrung ist dagegen nicht so einfach. Man kann durchaus
auf zwei bestimmten Wegen zum gleichen Ergebnis kommen, trotzdem muß
die Kraft nicht konservativ sein. Die Bedingung ist eben gerade,
daß man auf allen Wegen zum gleichen Ergebnis kommt.
Falls allerdings eine skalare Funktion 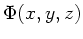 existiert, für
die
existiert, für
die
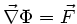 ist, so ist immer
ist, so ist immer
unabhängig vom Integrationsweg.
Aufgabe 2: Zeigen Sie, daß die Kraft 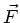 ein Potential besitzt, wenn
die folgenden Gleichungen erfüllt sind:
ein Potential besitzt, wenn
die folgenden Gleichungen erfüllt sind:
Diese drei Gleichungen von Aufgabe 2 geben uns also die Bedingung an, die
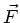 erfüllen muß, um eine konservative Kraft zu sein.
Abschließend geben wir noch ein Verfahren an, wie man das Potential
bestimmt, der Einfachheit halber für 2-dimensionale Felder
erfüllen muß, um eine konservative Kraft zu sein.
Abschließend geben wir noch ein Verfahren an, wie man das Potential
bestimmt, der Einfachheit halber für 2-dimensionale Felder
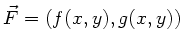 . Wir setzen also
. Wir setzen also 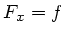 und
und 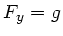 .
Es gilt nach Voraussetzung
.
Es gilt nach Voraussetzung
Aus der ersten Gleichung entnehmen wir, wobei 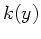 eine zunächst
beliebige Funktion ist,
eine zunächst
beliebige Funktion ist,
Differenziert man diesen Ansatz nach 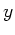 , so folgt
, so folgt
Andererseits sollte nach obiger Voraussetzung
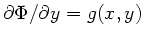 sein. Setzen wir dieses in die
vorherige Gleichung ein, so folgt für
sein. Setzen wir dieses in die
vorherige Gleichung ein, so folgt für 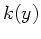 :
:
und nach unbestimmter Integration
Einsetzen von 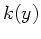 in die obige Gleichung für
in die obige Gleichung für 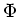 ergibt:
ergibt:
Im letzten Integral kann natürlich
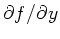 durch
durch
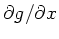 ersetzt werden. Diese Formel kann leicht
auf 3-dimensionale Felder verallgemeinert werden.
ersetzt werden. Diese Formel kann leicht
auf 3-dimensionale Felder verallgemeinert werden.
Aufgabe 3: Zeigen Sie, daß die Kraft
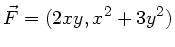 eine konservative Kraft ist und bestimmen Sie das Potential.
eine konservative Kraft ist und bestimmen Sie das Potential.
Lösungen zu den Rechenübungen am 4.12.2003
Vorbemerkung: In der Mathematik bezeichnet man häufig
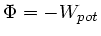 als Potential und
als Potential und
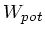 als potentielle Energie.
Darauf sollte noch einmal ausdrücklich hingewiesen werden.
als potentielle Energie.
Darauf sollte noch einmal ausdrücklich hingewiesen werden.
Aufgabe 1:
Es gilt z.B.
Entsprechend für die anderen Komponenten. Daraus folgt
Aufgabe 2:
Es gilt
Wir erhalten dann z.B.
Entsprechend für die anderen beiden Gleichungen.
Aufgabe 3:
Wegen
ist die Gleichung von Aufgabe 2 erfüllt. Wir benutzen die letzte Gleichung im Aufgabenblatt
und erhalten
Wir prüfen nochmal nach, dass wirklich gilt
Harm Fesefeldt
2007-08-02