Rechenübung am 21. Oktober 1999
Einige einfache Aufgaben
zur Addition von Geschwindigkeiten
Aufgabe 1:
Angenommen, Sie wollen senkrecht zum Ufer in 200 Sekunden über
einen 100 Meter breiten Fluss schwimmen.
Die Flussgeschwindigkeit des Wassers beträgt 1 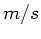 . Wie schnell
müssen Sie schwimmen können und in welche Richtung müssen Sie
schwimmen ?
. Wie schnell
müssen Sie schwimmen können und in welche Richtung müssen Sie
schwimmen ?
Aufgabe 2:
Ein Schiff segelt bei ruhigem Wasser mit einer Geschwindigkeit von
12 Knoten hart am Wind nach Westen. Der Wind kommt aus Südwesten mit einer
Geschwindigkeit von 3,5 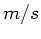 . Welche Windgeschwindigkeit und welche
Windrichtung relativ zur Fahrtrichtung messen Sie als Skipper auf dem
Schiff ?
. Welche Windgeschwindigkeit und welche
Windrichtung relativ zur Fahrtrichtung messen Sie als Skipper auf dem
Schiff ?
Aufgabe 3:
Ein Rheindampfer fährt zwischen zwei 100 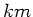 entfernten Orten hin und her.
Mit dem Strom braucht er 4 Stunden, gegen den Strom 10 Stunden. Wie groß
ist die Geschwindigkeit des Stromes und wie groß ist die Geschwindigkeit
des Dampfers relativ zum Wasser ?
entfernten Orten hin und her.
Mit dem Strom braucht er 4 Stunden, gegen den Strom 10 Stunden. Wie groß
ist die Geschwindigkeit des Stromes und wie groß ist die Geschwindigkeit
des Dampfers relativ zum Wasser ?
Aufgabe 4:
Ein (natürlich punktförmiger) Tintenfisch schläft in einer Ecke eines
rechtwinkligen Aquariums an der Wasseroberfläche. Das Aquarium ist 8 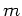 lang und 3
lang und 3 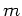 breit. Die Wassertiefe beträgt 2,5
breit. Die Wassertiefe beträgt 2,5 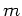 . In der Mitte des
Bodens befindet sich ein Futternapf.
. In der Mitte des
Bodens befindet sich ein Futternapf.
a) Wählen Sie ein geeignetes Koordinatensystem und geben Sie die
Komponenten des Vektors vom Tintenfisch zum Futternapf an !
b) Welche Strecke legt der Tintenfisch zurück, wenn er geradlinig zum
Futternapf schwimmt und welche Zeit benötigt er bis dahin bei einer
konstanten Geschwindigkeit von 30 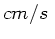 ?
?
c) Wie lang ist der kürzeste Weg, wenn er sich mit seinen Saugnäpfen
an den Wänden entlanghangelt und wie lange braucht er in diesem Fall
bei einer Geschwindigkeit von 10 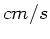 ?
?
Lösungen zu den Rechenübungen Nr.1
am 21. Oktober 1999
Aufgabe 1:
Bezeichnen wir die Flussgeschwindigkeit mit 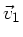 und die Schwimmgeschwindigkeit relativ zum Wasser mit
und die Schwimmgeschwindigkeit relativ zum Wasser mit 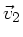 ,
so ergibt sich die Gesamtgeschwindigkeit zu
,
so ergibt sich die Gesamtgeschwindigkeit zu
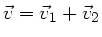 .
.
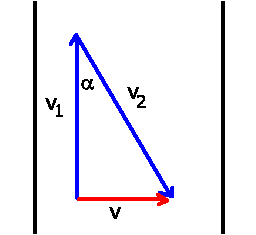
Mit
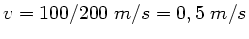 und
und
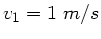 folgt
folgt
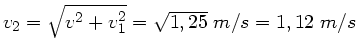 .
Der Winkel beträgt
.
Der Winkel beträgt
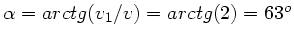 .
.
Aufgabe 2:
Bei der Umrechnung von Knoten in 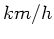 bzw
bzw 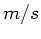 muss zwischen Landmeile
( = 1,63
muss zwischen Landmeile
( = 1,63 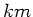 ) und nautischer Meile ( = 1,85
) und nautischer Meile ( = 1,85 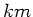 ) unterschieden werden.
Bei der Einheit Knoten ist offensichtlich die nautische Meile gemeint.
Daher gilt:
) unterschieden werden.
Bei der Einheit Knoten ist offensichtlich die nautische Meile gemeint.
Daher gilt:
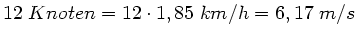 .
Wir wählen ein Koordinatensystem mit x-Achse noch Osten und y-Achse
nach Norden:
.
Wir wählen ein Koordinatensystem mit x-Achse noch Osten und y-Achse
nach Norden:
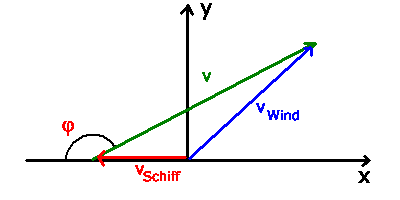
Schiff und Wind haben die Geschwindigkeiten:
Der auf dem Schiff gemessene scheinbare Wind ist
Daraus folgt
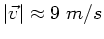 .
.
Das Skalarprodukt beider Vektoren ist
Der Winkel zwischen scheinbarem Wind und Fahrtrichtung ist damit:
Also:
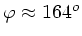 .
.
Aufgabe 3:
Sei 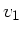 die Geschwindigkeit des Stromes und
die Geschwindigkeit des Stromes und 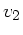 die
Geschwindikeit des Dampfers relativ zum Wasser, so gilt mit
die
Geschwindikeit des Dampfers relativ zum Wasser, so gilt mit 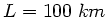
Aufgelöst nach 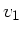 und
und 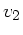 folgt:
folgt:
Aufgabe 4:
a) In einem rechtwinkligen Koordinatensystem stellen wir Tintenfisch und
Futternapf als Vektoren dar:
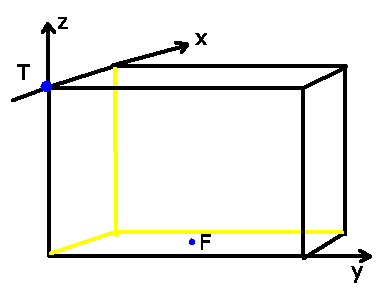
b) Der direkte Weg wird durch den Vektor
beschrieben, mit der Länge
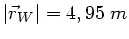 . Die Zeit
beträgt
. Die Zeit
beträgt
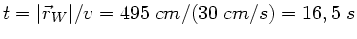 .
.
c) Um den kürzesten Weg zu finden, klappen wir die Seitenwände einfach
auf,
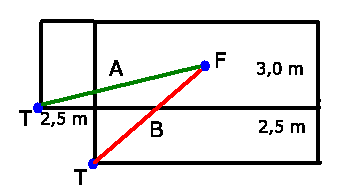
Wir erhalten dann zwei Möglichkeiten, Weg A oder Weg B, von denen der
zweite mit 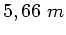 Länge offensichtlich der kürzere ist.
Daher
Länge offensichtlich der kürzere ist.
Daher
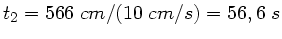 .
.
Harm Fesefeldt
2007-08-02


![]() und
und
![]() folgt
folgt
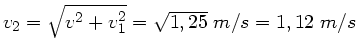 .
Der Winkel beträgt
.
Der Winkel beträgt
![]() .
. ![]() bzw
bzw ![]() muss zwischen Landmeile
( = 1,63
muss zwischen Landmeile
( = 1,63 ![]() ) und nautischer Meile ( = 1,85
) und nautischer Meile ( = 1,85 ![]() ) unterschieden werden.
Bei der Einheit Knoten ist offensichtlich die nautische Meile gemeint.
Daher gilt:
) unterschieden werden.
Bei der Einheit Knoten ist offensichtlich die nautische Meile gemeint.
Daher gilt:
![]() .
Wir wählen ein Koordinatensystem mit x-Achse noch Osten und y-Achse
nach Norden:
.
Wir wählen ein Koordinatensystem mit x-Achse noch Osten und y-Achse
nach Norden: 
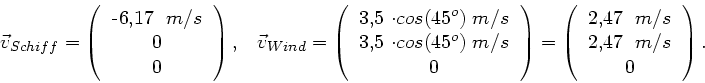
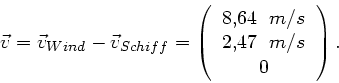
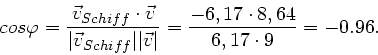
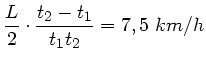
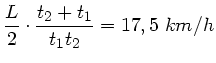

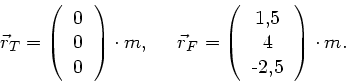
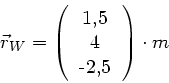

![]() Länge offensichtlich der kürzere ist.
Daher
Länge offensichtlich der kürzere ist.
Daher
![]() .
.