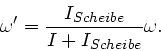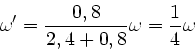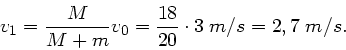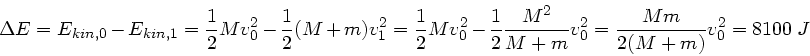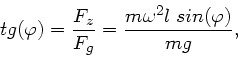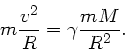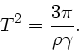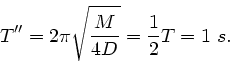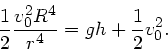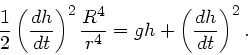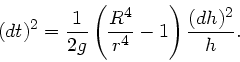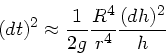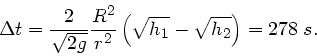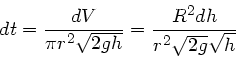Lösungen zur Klausur
Besprechung: Donnerstag, den 3. Februar 2000
Aufgabe 1: (8 Punkte)
a) Wegen Drehimpulserhaltung gilt:
wobei 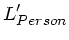 und
und 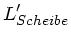 die Drehimpulse der Person und der
Scheibe nach dem Abbremsen sind. Daher gilt auch
die Drehimpulse der Person und der
Scheibe nach dem Abbremsen sind. Daher gilt auch
oder
Das Trägheitsmoment der Scheibe ist
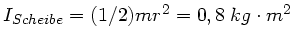 , daher
, daher
oder auch
b) Die Rotationsenergie ist:
Aufgabe 2: (9 Punkte)
a) Dieses ist ein inelastischer Vorgang, d.h. man kann nur den Impulssatz,
nicht den Energiesatz anwenden:
wobei
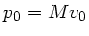 der Impuls des Wagens ohne Sand und
der Impuls des Wagens ohne Sand und
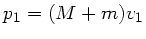 der Impuls des Wagens mit Sand ist. Ausserdem
ist
der Impuls des Wagens mit Sand ist. Ausserdem
ist 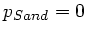 . Also gilt
. Also gilt 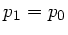 oder
oder
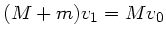 . Aufgelöst nach
. Aufgelöst nach 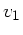 folgt:
folgt:
b) Die Energiedifferenz ist
Diese Energie geht in Reibungswärme verloren, wenn der Sand sich auf dem
Boden des Wagens reibt. Der Sand muss ja in Fahrtrichtung beschleunigt
werden.
c) Nach Ausschütten des Sandes ändert sich die Geschwindigkeit des
Wagens nicht. Der Sand nimmt seinen Impuls mit.
oder
Die Geschwindigkeit des Wagens bleibt
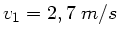 .
.
Aufgabe 3: (8 Punkte)
a) Im Gleichgewicht muss die resultierend Kraft aus der Schwerkraft
und der Zentrifugalkraft in Richtung der Stange zeigen,
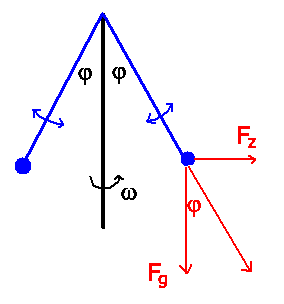
Daher folgt:
oder
oder
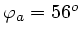 .
.
b) In diesem Fall erhält man
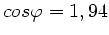 , d.h. keine reelle
Lösung. Die Grenzfrequenz für
, d.h. keine reelle
Lösung. Die Grenzfrequenz für
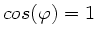 ist
ist
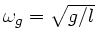 , d.h. die Frequenz der Pendelschwindung.
Für kleinere Frequenzen gibt es keine Auslenkung mehr, d.h.
, d.h. die Frequenz der Pendelschwindung.
Für kleinere Frequenzen gibt es keine Auslenkung mehr, d.h.
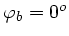 .
.
Aufgabe 4: (8 Punkte)
Die Zentrifugalkraft muss der Gravitationskraft das Gleichgewicht halten,
Mit
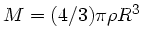 und
und
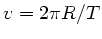 folgt:
folgt:
Die Umlaufzeit hängt nicht vom Radius des Planeten ab.
Aufgabe 5: (8 Punkte)
Die beiden Hälften haben die Federkonstante 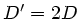 , wenn
, wenn 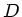 die
Federkonstante der ursprünglichen Feder war (siehe Übung 3, Nr.1).
Daher gilt
die
Federkonstante der ursprünglichen Feder war (siehe Übung 3, Nr.1).
Daher gilt
und
Aufgabe 6: (9 Punkte)
Allgemein kann man den Ansatz machen:
Mit 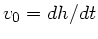 und
und
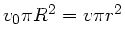 folgt:
folgt:
oder
Daraus folgt
Da
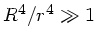 , kann man auch schreiben:
, kann man auch schreiben:
Integration ergibt:
Einfacher geht es natürlich, wenn man die in der Vorlesung abgeleitete
Formel für die Ausflussgeschwindigkeit noch im Kopf hat:
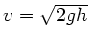 . Mit
. Mit
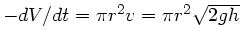 folgt sofort
folgt sofort
Integration liefert das selbe Ergebnis wie oben.
Harm Fesefeldt
2007-08-02