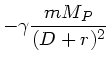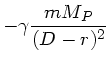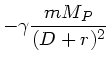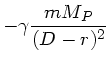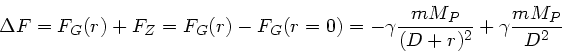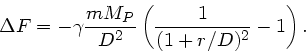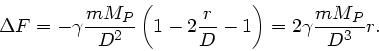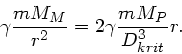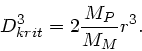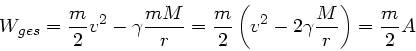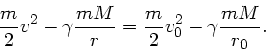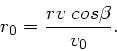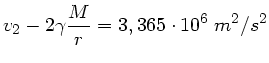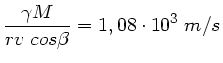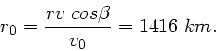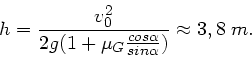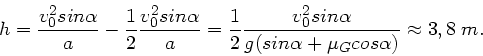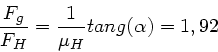Übung Nr. 9
Abgabetermin: Donnerstag, den 13. Januar 2000
Aufgabe 1: (8 Punkte)
Die Kraft auf ein Massenelement  in den Punkten
in den Punkten  und
und  ist
ist
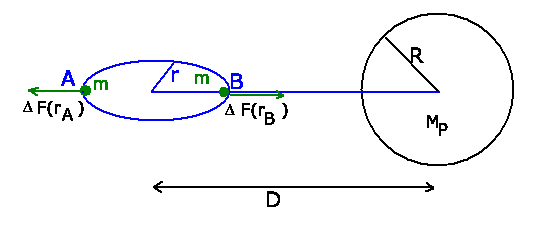
Die Differenz zur Fliehkraft ist für Punkt A:
Dieses kann man auch schreiben als
Wegen
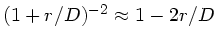 folgt näherungsweise für
folgt näherungsweise für
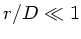 :
:
Der Mond ist stabil, solange die Anziehungskraft des Mondes auf die Masse
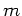 größer als die Gezeitenkraft des Planeten ist. Die Grenzbedingung
lautet also
größer als die Gezeitenkraft des Planeten ist. Die Grenzbedingung
lautet also
oder
Mit
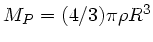 und
und
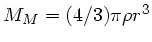 können wir auch schreiben:
können wir auch schreiben:
oder
Der exakte Wert ist
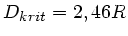 , also ungefähr einen Faktor
2 größer.
, also ungefähr einen Faktor
2 größer.
Aufgabe 2: (7 Punkte)
Die Gesamtenergie ist auf der gesamten Bahn konstant und im Punkte des
Aufpralls auf dem Mond gegeben durch
Die Bahnkonstante 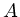 können wir ausrechen zu
können wir ausrechen zu
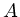 ist insbesondere größer Null, daher ist die Gesamtenergie größer
Null und die Bahn eine Hyperbel.
ist insbesondere größer Null, daher ist die Gesamtenergie größer
Null und die Bahn eine Hyperbel.
b) Die Energieerhaltung verlangt
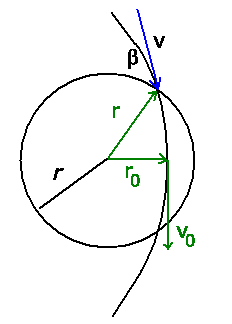
Eine zweite Gleichung erhalten wir aus der Drehimpulserhaltung:
oder
Dieses setzen wir in die Energiegleichung ein und erhalten nach kurzer
Umformung
mit
Insgesamt also
Der Meteorit katte beim Aufprall also praktisch schon seine höchste
Geschwindigkeit.
c) Den minimalen Abstand berechnen wir aus
Aufgabe 3: (5 Punkte)
a) Beim ersten Teil dieser Aufgabe gibt es zwei Lösungswege:
1. Lösungsweg
Die Auflagekraft ist
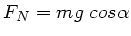 , die Gleitreibungskraft
daher
, die Gleitreibungskraft
daher
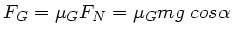 . Auf dem Weg
. Auf dem Weg
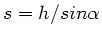 wird also die Arbeit
wird also die Arbeit
verbraten. Der Energiesatz lautet hiermit:
Aufgelöst nach 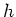 ergibt:
ergibt:
2. Lösungsweg
Der zweite Lösungsweg ist etwas komplizierter und vermeidet den
Energiesatz. Die Bewegungsgleichung des Klotzes auf der schiefen Ebene ist
Mit
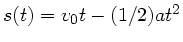 und
und
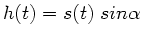 folgt:
folgt:
Die maximale Höhe wird erreicht, wenn 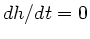 wird, daraus folgt
die hierzu notwendige Zeit
wird, daraus folgt
die hierzu notwendige Zeit
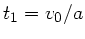 . Einsetzen in die vorherige
Formel liefert:
. Einsetzen in die vorherige
Formel liefert:
b) Das Verhältnis der rücktreibenden Schwerkraft
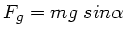 zur Haftreibungskraft
zur Haftreibungskraft
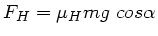 ,
,
ist größer als 1, daher gleitet der Klotz die Ebene wieder herunter.
Harm Fesefeldt
2007-08-02