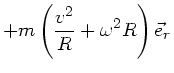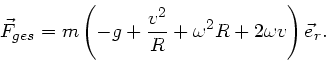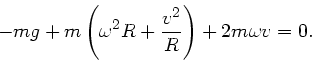Lösungen zur Übung Nr. 7
Besprechung: Donnerstag, den 9. Dezember 1999
Aufgabe 1: (6 Punkte)
a) Beim Laufen in Fahrtrichtung des Zuges sind Zentrifugalkraft und
Corioliskraft gleichgerichtet, daher
b) Beim Laufen entgegengesetzt zur Fahrtrichtung kehrt sich das Vorzeichen
der Corioliskraft um, daher
Bei typischen Geschwindigkeiten von
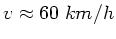 und
und
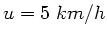 beträgt der Unterschied in den Trägheitskräften
also bereits
beträgt der Unterschied in den Trägheitskräften
also bereits 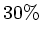 .
.
Aufgabe 2: (7 Punkte)
a) Die Geschwindigkeit 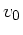 des Pendels beim Nulldurchgang ist mit Hilfe
des Energiesatzes durch
des Pendels beim Nulldurchgang ist mit Hilfe
des Energiesatzes durch
oder
gegeben, daher
Die wirksame Komponente 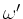 der Winkelgeschwindigkeit am Ort der
geographischen Breite
der Winkelgeschwindigkeit am Ort der
geographischen Breite 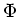 ist
ist
mit der Dauer eines Sterntages
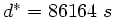 , was sich
geringfügig von
, was sich
geringfügig von
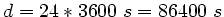 unterscheidet. Daher
folgt für die Corioliskraft beim Nulldurchgang:
unterscheidet. Daher
folgt für die Corioliskraft beim Nulldurchgang:
b) Die Corioliskraft ist gleich der Zentrifugalkraft der horizontalen
Bewegung, d.h
Daraus berechnen wir den Krümmungsradius zu
c) Eine volle Drehung erhält man für
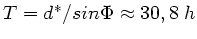 .
.
Aufgabe 3: (7 Punkte)
Wenn der Wagen steht, wirken nur die Schwerkraft und Zentrifugalkraft,
Insgesamt also
b) Entlang des Äquators in Ost- Richtung wirken die drei Kräfte
Zu beachten ist hierbei, dass bei Fahrt in Ost-Richtung auch die
Zentrifugalbeschleunigung erhöht wird, da sich auch die Erde in
Ost-Richtung dreht. Insgesamt also
c) Damit der Wagen abhebt, muss die Summe aller auf ihn wirkenden Kräfte
verschwinden, d.h.
Aufgelöst nach der Geschwindigkeit 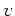 ergibt sich
ergibt sich
Harm Fesefeldt
2007-08-02