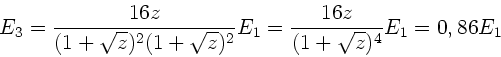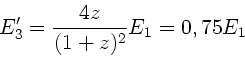Physik I, WS 1993/94
Lösungen zur Übung Nr. 3
Besprechung: 18. November 1993
Aufgabe 1: (Bonusaufgabe) (5 Punkte)
Am einfachsten löst man diese Aufgabe in einem Koordinatensystem mit
der schiefen Ebene als x-Achse:
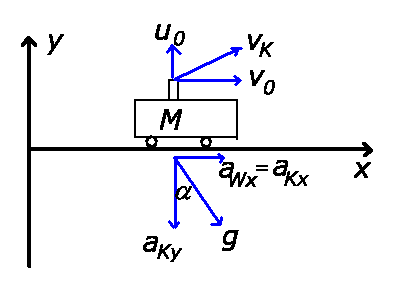
Die Beschleunigung des Wagens ist dann
und die Beschleunigung der Kugel
Man sieht also, daß Wagen und Kugel in der x-Projektion exakt gleich
laufen, da beide beim Abschuß der Kugel die gleiche
Geschwindigkeitskomponente hatten,
Daraus folgt, daß die Kugel auf die Rohrmündung zurückfallen muß.
Die Zeit des Aufpralls folgt aus der Bewegungsgleichung der y- Komponente.
Integration der zweiten Gleichung:
Die Bedingung 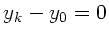 ergibt die Lösungen
ergibt die Lösungen 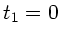 (Abschuß)
und
(Abschuß)
und
Aufgabe 2: (5 Punkte)
a) Wir setzen den Nullpunkt der potentiellen Energie der Kugel auf die
Koordinate der maximal verkürzten Feder. Dann erhalten wir die
Gesamtenergien 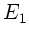 am Anfang der Bewegung und
am Anfang der Bewegung und 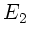 am Ende der
Bewegung zu
am Ende der
Bewegung zu
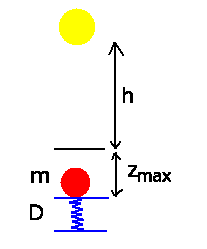
Wegen Energieerhaltung müssen beide übereinstimmen:
Aufgelöst nach 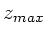 :
:
Da wir nach der Verkürzung gefragt haben, also
b) Bei einer beliebigen Verkürzung der Feder gilt für die kinetische
Energie:
Die Richtigkeit dieser Formel erkennt man aus den Werten für 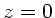 und
und
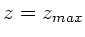 .
Aus der Extremalbedingung
.
Aus der Extremalbedingung
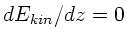 rechnet man aus, daß
die maximale kinetische Energie und damit Geschwindigkeit bei
rechnet man aus, daß
die maximale kinetische Energie und damit Geschwindigkeit bei
auftritt. Für die gesamte Fallstrecke ergibt dieses
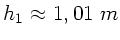 .
.
c) Die kinetische Energie bei dieser Fallstrecke ist
und die Geschwindigkeit
Aufgabe 3: (4 Punkte)
Aufgabe 4: (5 Punkte)
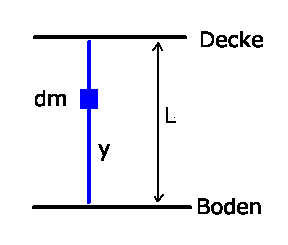
Während das Seil auf den Boden fällt, wirken zwei Kräfte:
Erstens das Gewicht von dem bereits auf dem Boden liegenden Teil des
Seils und zweitens die durch den Impulsverlust des herunterfallenden
Seils erzeugte Kraft. Hierbei handelt es sich um einen vollständig
inelastischen Stoß. Ein Element des Seils hat die Masse
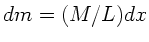 . Der Impulsverlust dieses Massenelementes erzeugt die
Kraft
. Der Impulsverlust dieses Massenelementes erzeugt die
Kraft
Hierbei ist 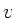 die Geschwindigkeit, mit der ein Massenelement den Boden
erreicht,
die Geschwindigkeit, mit der ein Massenelement den Boden
erreicht, 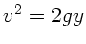 .
. 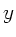 ist die Länge des Seilstückes, das bereits
auf dem Boden liegt und damit die Höhe, aus dem dieses Massenelement
unter dem Einfluß der Schwerkraft heruntergefallen ist.
ist die Länge des Seilstückes, das bereits
auf dem Boden liegt und damit die Höhe, aus dem dieses Massenelement
unter dem Einfluß der Schwerkraft heruntergefallen ist.
Wir erhalten also die vom Impulsverlust erzeugte Kraft
Die Gesamtkraft ergibt sich aus der Summe dieser Kraft und dem Gewicht
des bereits auf dem Boden liegenden Teil des Seilstückes
Das Verhältnis der Gesamtkraft zu dem bereits auf dem Boden liegenden
Gewicht ist also
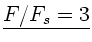 .
.
Aufgabe 5: (6 Punkte)
Nach Vorlesung ist bei einem zentralen elastischen Stoß die
Geschwindigkeit der Kugeln nach dem Stoß:
Die Energie der zweiten Kugel ist also
Im letzten Schritt haben wir 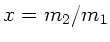 eingesetzt. Entsprechend
gilt beim Stoß der zweiten Kugel mit der dritten Kugel:
eingesetzt. Entsprechend
gilt beim Stoß der zweiten Kugel mit der dritten Kugel:
mit 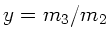 . Daher
. Daher
Nach Anleitung setzen wir
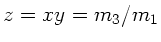 , wobei
, wobei 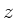 in der nachfolgenden
Extremalaufgabe eine Konstante ist:
in der nachfolgenden
Extremalaufgabe eine Konstante ist:
Statt das Maximum aus der Extremalbedingung 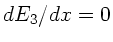 zu suchen,
ist es hier einfacher, das Minimum aus
zu suchen,
ist es hier einfacher, das Minimum aus 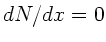 zu bestimmen, wobei
zu bestimmen, wobei 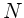 der Nenner des obigen Ausdrucks ist, also
der Nenner des obigen Ausdrucks ist, also
Die Auswertung ergibt
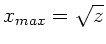 oder
oder
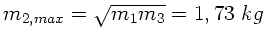 .
.
b) Die Energie der dritten Kugel berechnet sich zu:
c) Beim direkten Stoß der ersten mit der dritten Kugel ist (siehe oben)
Man sieht also, daß der Energieübertrag von der ersten auf die dritte
größer wird, wenn man eine Kugel mit der Masse
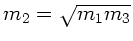 dazwischen schaltet.
dazwischen schaltet.
Harm Fesefeldt
2007-08-06


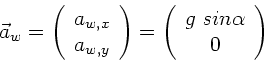
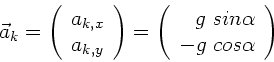
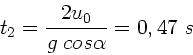
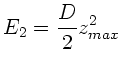

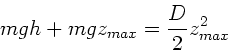
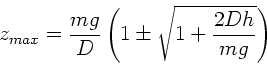
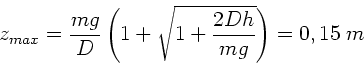
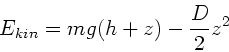
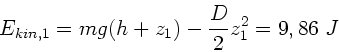
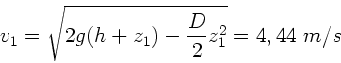
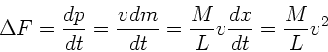

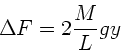
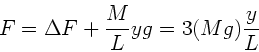

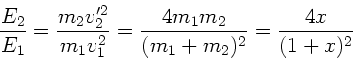
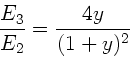
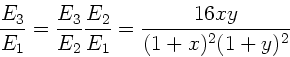
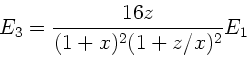
![\begin{displaymath}
\frac{d}{dx} \left[ (1+x)^{2} (1+z/x)^{2} \right] = 0
\end{displaymath}](img46.gif)