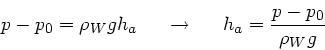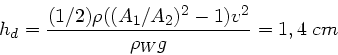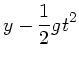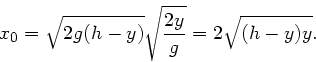Lösungen zur Übung Nr.11
Besprechung: Donnerstag 22.Januar 2004
Aufgabe 1: (8 Punkte)
a) Die frei werdende Energie ist
Ausserdem gilt
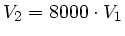 oder
oder
Damit wird
b) Für die Arbeit, den Radius einer Kugel um 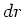 zu vergrößern, erhalten wir einmal
zu vergrößern, erhalten wir einmal
zum anderen auch über
Aus beiden Gleichungen folgt
Angewendet auf die beiden Kugeln folgt
Man beachte also, dass 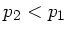 , wie in der Vorlesung auch am Beispiel von Seifenblasen
demonstriert wurde (''Die Großen schlucken die Kleinen'').
, wie in der Vorlesung auch am Beispiel von Seifenblasen
demonstriert wurde (''Die Großen schlucken die Kleinen'').
c) Die Depression in einem einzelnen Rohr ist nach Vorlesung
Bei Quecksilber kann man völlige Nichtbenetzung annehmen, d.h. 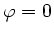 und
und
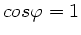 .
Dieses folgt auch aus der Annahme von Teil a) und b), dass die Tropfen Kugelform haben.
Wir denken uns die beiderseits offenen Rohre zunächst getrennt und tauchen sie in einen unendlich
grossen Hg- Behälter.
.
Dieses folgt auch aus der Annahme von Teil a) und b), dass die Tropfen Kugelform haben.
Wir denken uns die beiderseits offenen Rohre zunächst getrennt und tauchen sie in einen unendlich
grossen Hg- Behälter.
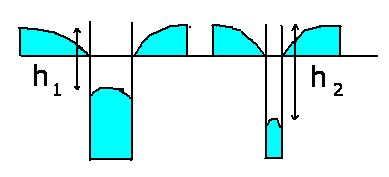
Dann gilt für die einzelnen Rohre:
Anschliessend verbindet man die Rohre zu einem U-Rohr und entfernt den unendlich grossen
Behälter. Die Differenz bleibt dabei erhalten:
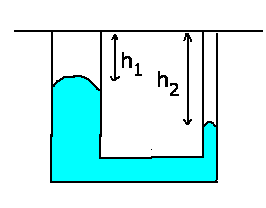
Aufgabe 2: (8 Punkte)
In Teil a) misst man die Differenz zwischen dem statischen Druck
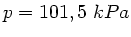 und dem
äusseren Luftdruck
und dem
äusseren Luftdruck
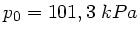 ,
,
oder
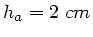 .
.
Im Fall b) muss der Unterschied zwischen Gesamtdruck und äusserer Luftdruck bestimmt werden,
Man sieht, dass der Staudruck hier keine grosse Änderung hervorruft. Fall c) gibt einfach
also fast unmessbar. Im Fall d) schliesslich wird die Differenz der statischen Drücke
gemessen. Daher gilt
Mit
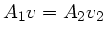 folgt
folgt
Aufgabe 3: (4 Punkte)
Die Ausströmgeschwindigkeit ist wegen Bernoulli (
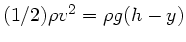 ) durch
) durch
gegeben. Die Bewegung des Wassers entspricht einem horizontalen Wurf, daher
Für 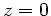 erhalten wir die Weite
erhalten wir die Weite 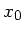
Damit dieses maximal wird, muss einfach 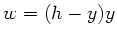 maximal werden.
Die Maximalbedingung lautet daher einfach
maximal werden.
Die Maximalbedingung lautet daher einfach
Dieses konnten wir auch im Experiment in der Vorlesung beobachten.
Harm Fesefeldt
2007-08-01
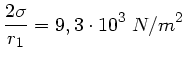
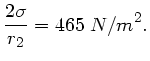
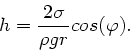

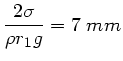
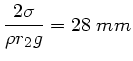

![]() und dem
äusseren Luftdruck
und dem
äusseren Luftdruck
![]() ,
,