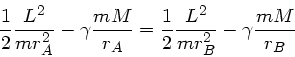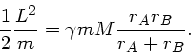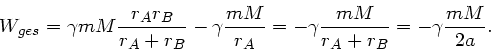Lösungsvorschläge zur Übung Nr.8
Besprechung: Donnerstag 8.Januar 2004
Aufgabe 1: (7 Punkte)
Erde und Mond bewegen sich auf Kreisbahnen um ihren gemeinsamen Schwerpunkt, daher
gilt
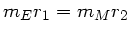 . Mit
. Mit
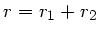 folgt
folgt
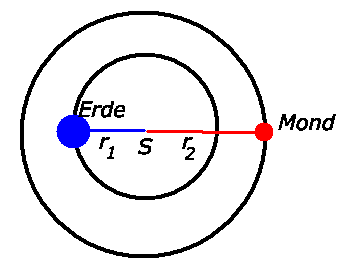
Das Bewegungszentrum liegt also noch innerhalb der Erdkugel. Diese 380000  werden
üblicherweise als Abstand von Erde und Mond angegeben. Das ist ersichtlich nicht ganz
richtig.
werden
üblicherweise als Abstand von Erde und Mond angegeben. Das ist ersichtlich nicht ganz
richtig.
b) Die Umlaufdauer des Mondes wird über die Bewegungsgleichung
bestimmt. Hier muss man jetzt aufpassen. Im Gravitationsgesetz steht der Abstand
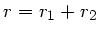 zwischen Mond und Erde, während die Radialbeschleunigung
des Mondes durch
zwischen Mond und Erde, während die Radialbeschleunigung
des Mondes durch
gegeben ist. Damit findet man
Aufgabe 2: (7 Punkte)
Beim Vorschlag von Obelix wird die für die Kreisbewegung erforderliche Radialkraft durch
die Gravitationskraft kompensiert
Die erforderliche Geschwindigkeit ist
und die halbe Umlaufzeit beträgt
Beim letzten Schritt wurde
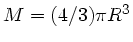 gesetzt.
Der Vorschlag von Asterix ist genau so einfach.
Die Kraft auf die Rohrpost beim Abstand
gesetzt.
Der Vorschlag von Asterix ist genau so einfach.
Die Kraft auf die Rohrpost beim Abstand 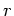 vom Ermittelpunkt ist
vom Ermittelpunkt ist
Die DGL ist
Diese Gleichung ist uns wohlbekannt, nämlich die Schwingungsgleichung. Wir erhalten
und daher die halbe Schwingungsdauer
Die Zeiten sind also in beiden Fällen gleich.
Aufgabe 3: (6 Punkte)
Wir wählen einen Kreisring der Dicke 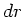 und Radius
und Radius 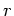 :
:
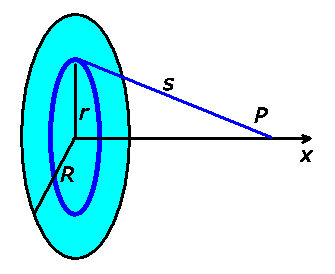
Dieser hat die Masse
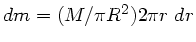 und erzeugt am Punkt
und erzeugt am Punkt 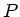 den
Beitrag
den
Beitrag
zum Potential. Integration über die gesamte Fläche ergibt:
Für die Feldstärke gilt nach Vorlesung
wobei wir den Einheitsvektor in  - Richtung eingeführt haben. Daher
- Richtung eingeführt haben. Daher
Das Minuszeichen besagt, dass die Feldstärke zur Platte hin gerichtet ist.
Aufgabe 4: (Bonusaufgabe) (5 Punkte)
Die Formel (5) auf Seite 115 des Skripts lautet in den Schnittpunkten der großen Halbachse
mit der Ellepsenbahn (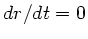 in den Punkten
in den Punkten 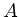 und
und 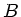 ):
):
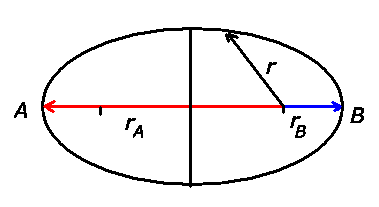
Der Drehimpuls ist konstant, ist in den Punkten 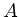 und
und 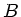 also gleich. Da auch die
Gesamtenergie während der Bewegung konstant ist, gilt:
also gleich. Da auch die
Gesamtenergie während der Bewegung konstant ist, gilt:
Für den Drehimpuls erhalten wir
Einsetzen dieses Ausdrucks in die Formel für 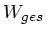 ergibt:
ergibt:
Harm Fesefeldt
2007-08-01
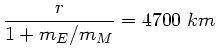
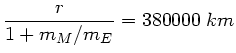
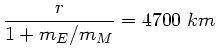
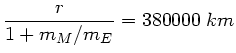

![]() werden
üblicherweise als Abstand von Erde und Mond angegeben. Das ist ersichtlich nicht ganz
richtig.
werden
üblicherweise als Abstand von Erde und Mond angegeben. Das ist ersichtlich nicht ganz
richtig. 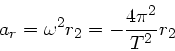
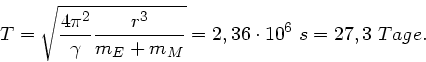
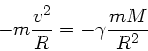
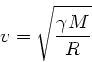
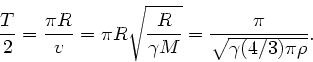
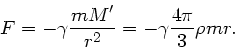
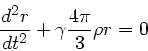
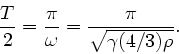

![]() und erzeugt am Punkt
und erzeugt am Punkt ![]() den
Beitrag
den
Beitrag
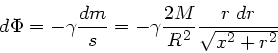
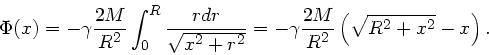
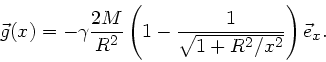
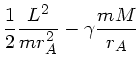
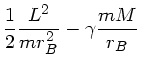

![]() und
und ![]() also gleich. Da auch die
Gesamtenergie während der Bewegung konstant ist, gilt:
also gleich. Da auch die
Gesamtenergie während der Bewegung konstant ist, gilt: