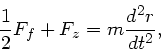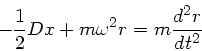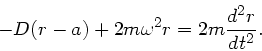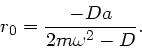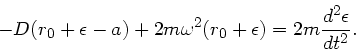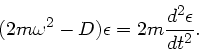Lösungsvorschläge zur Übung Nr.5
Besprechung: Donnerstag 4.Dezember 2003
Aufgabe 1: (5 Punkte)
Es handelt sich um einen zentralen, elastischen Stoß, daher erhalten wir für die Geschwindigkeiten
der beiden Massen nach dem Stoß:
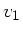 folgt aus dem Energiesatz (
folgt aus dem Energiesatz (
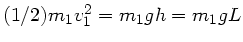 ) zu
) zu
a) Einsetzen ergibt
b) Die kinetische Energie der Masse 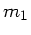 nach dem Stoß,
nach dem Stoß,
wird beim Maximalausschlag umgesetzt in potentielle Energie
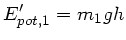 ,
,
oder
Der Winkel schliesslich ist(
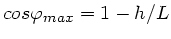 ):
):
Aufgabe 2: (7 Punkte)
a) Aus der Abbildung folgt:
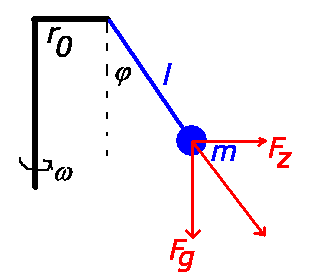
oder
Dieses ist eine transzendente Gleichung, die wir graphisch lösen:
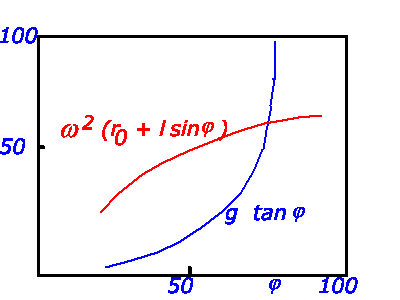
Die Näherungslösung ist
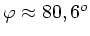 .
.
b) Für 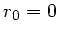 ist
ist
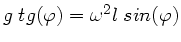 oder
oder
In dieser Formel ist
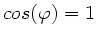 und damit
und damit 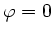 für die Grenzfrequenz
für die Grenzfrequenz
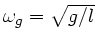 . Dieses ist genau die Frequenz des linearen zweidimensionalen Pendels,
das System geht in eine zweidimensionale Schwingung über. Physikalisch bedeutet das,
dass die Komponente der Schwerkraft senkrecht zum Pendel grundsätzlich größer wird als die
Komponente der Fliehkraft.
. Dieses ist genau die Frequenz des linearen zweidimensionalen Pendels,
das System geht in eine zweidimensionale Schwingung über. Physikalisch bedeutet das,
dass die Komponente der Schwerkraft senkrecht zum Pendel grundsätzlich größer wird als die
Komponente der Fliehkraft.
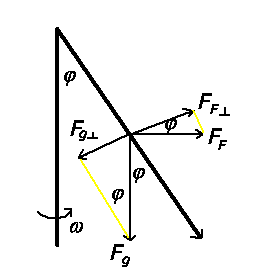
Mit
gilt für
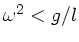 die Abschätzung:
die Abschätzung:
also
Aufgabe 3 (8 Punkte)
Zur Lösung der Aufgabe setzt man für einen der Wagen die Kraftgleichung aus Federkraft 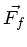 und
Zentrifugalkraft
und
Zentrifugalkraft 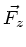 an:
an:
wobei 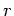 die Position des Wagens auf der Schiene von der Drehachse aus gemessen ist. Wir brauchen keine Vektoren
zu schreiben, da beide Kräfte in Richtung von
die Position des Wagens auf der Schiene von der Drehachse aus gemessen ist. Wir brauchen keine Vektoren
zu schreiben, da beide Kräfte in Richtung von 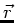 zeigen. Auf einen der beiden Wagen wirkt nur die
halbe Federkraft. Daher gilt:
zeigen. Auf einen der beiden Wagen wirkt nur die
halbe Federkraft. Daher gilt:
Mit 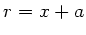 können wir auch schreiben:
können wir auch schreiben:
Als erstes bestimmen wir die Gleichgewichtslage 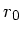 des Wagens. In diesem Fall wirkt keine Beschleunigung, also
des Wagens. In diesem Fall wirkt keine Beschleunigung, also
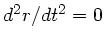 und
und
Da 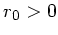 sein muss, existiert nur eine Gleichgewichtslage für
sein muss, existiert nur eine Gleichgewichtslage für 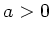 und
und
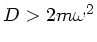 (1. Fall) oder
(1. Fall) oder
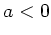 und
und
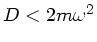 (2. Fall). Für
(2. Fall). Für
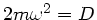 und
und 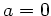 ist der Wagen immer im Gleichgewicht
(indifferentes Gleichgewicht).
ist der Wagen immer im Gleichgewicht
(indifferentes Gleichgewicht).
Zur Untersuchung der Stabilität der Gleichgewichtslagen lenken wir den Wagen um eine kleine
Strecke 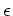 aus und untersuchen die Reaktion des Wagens auf diese Störung.
aus und untersuchen die Reaktion des Wagens auf diese Störung.
Die Bewegungsgleichung wird zu
Setzt man noch für 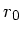 die bereits oben angeschriebene Lösung ein, so folgt nach einigen Umformungen die DGL
die bereits oben angeschriebene Lösung ein, so folgt nach einigen Umformungen die DGL
Falls
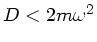 (2. Fall) wird der Wagen bei einer positiven Auslenkung
(2. Fall) wird der Wagen bei einer positiven Auslenkung 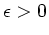 weiter nach aussen beschleunigt
(
weiter nach aussen beschleunigt
(
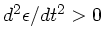 ). Dieser Fall ist also instabil.
). Dieser Fall ist also instabil.
Falls
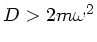 (1. Fall) wird der Wagen bei einer positiven Auslenkung
(1. Fall) wird der Wagen bei einer positiven Auslenkung 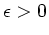 zurück nach innen,
also zur Gleichgewichtslage hin, beschleunigt (
zurück nach innen,
also zur Gleichgewichtslage hin, beschleunigt (
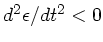 ). Dieser Fall ist also stabil und kann als
Fliehkraftregler benutzt werden.
). Dieser Fall ist also stabil und kann als
Fliehkraftregler benutzt werden.
Harm Fesefeldt
2007-08-01
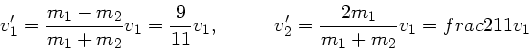
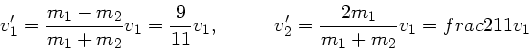
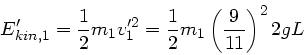
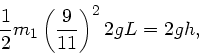
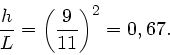

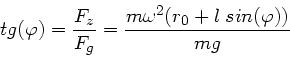

![]() .
. ![]() ist
ist
![]() oder
oder