Lösungsvorschläge zur Übung Nr.2
Besprechung: Donnerstag 13.November 2003
Aufgabe 1: (5 Punkte)
Um diese Aufgabe allgemein zu lösen, diskutieren wir zunächst die Hintereinanderschaltung und
Parallelschaltung zweier beliebiger Federn mit Feserkonstanten 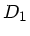 und
und 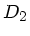 .
Bei der Hintereinanderschaltung (Serienschaltung) ist die Kraft in der gesamten Feder gleich.
Daher folgt:
.
Bei der Hintereinanderschaltung (Serienschaltung) ist die Kraft in der gesamten Feder gleich.
Daher folgt:
wobei noch
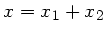 .
.
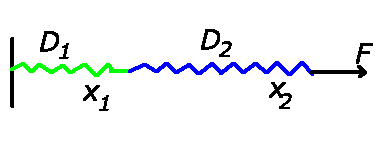
Diese Gleichungen können umgeformt werden zu
Daher ist also
oder auch
Bei der Parallelschaltung teilt sich die angreifende Kraft auf die beiden Federn auf, sofern
die Länge bei der Nullpunktslage übereinstimmt.
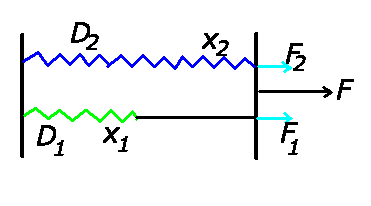
Daher
Mit
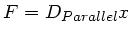 und
und
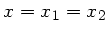 erhält man in diesem Fall einfach
erhält man in diesem Fall einfach
Also
Die Serien- und Parallelschaltung von Widerständen in der Elektrizitätslehre läßt
grüßen ! Und nun zur eigentlichen Aufgabe:
! Und nun zur eigentlichen Aufgabe:
a) Die Serienschaltung zweier gleicher Federn ist
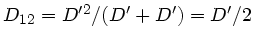 , daher
folgt für die Serienschaltung dreier gleicher Ferdern:
, daher
folgt für die Serienschaltung dreier gleicher Ferdern:
Daher sind die Federkonstanten der drei Einzelteile 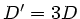 .
.
b) Zwei Federteile parallel und eine dahinter in Serie ergibt
Aufgabe 2: (6 Punkte)
Zur Lösung dieser Aufgabe führt man am besten ein neues Bezugssystem ein, bei dem
die 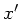 - Achse entlang des Bergs zeigt und
- Achse entlang des Bergs zeigt und 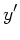 dazu senkrecht steht. In diesem System ist
die Geschwindigkeit des Balls beim Abschuss
dazu senkrecht steht. In diesem System ist
die Geschwindigkeit des Balls beim Abschuss
und die Gravitationsbeschleunigung
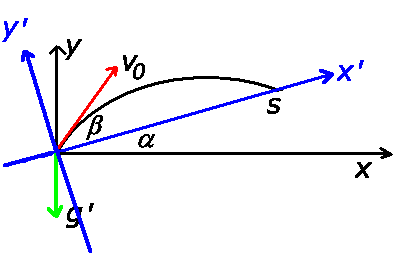
Der Ortsvektor der Flugbahn ist dann im gestrichenen System
Der Ball trifft auf den Abhang, wenn 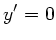 wird. Daraus folgt die Zeit bis zum Auftreffen:
wird. Daraus folgt die Zeit bis zum Auftreffen:
und die Strecke 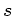 zu
zu
Aus der Extremalbedingung 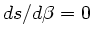 folgt nach einigen Umformungen
folgt nach einigen Umformungen
oder
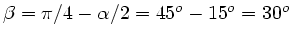 .
.
Aufgabe 3: (4 Punkte)
Die Seilspannung im Teilstück 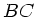 ist
ist 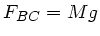 . Im Teilstück
. Im Teilstück 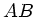 sollte sie
doppelt so groß sein, also
sollte sie
doppelt so groß sein, also 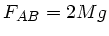 . Aus der Geometrie folgt bei
. Aus der Geometrie folgt bei 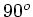 , dass
, dass
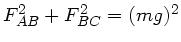 . Daher folgt
. Daher folgt
oder
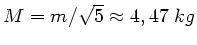 .
.
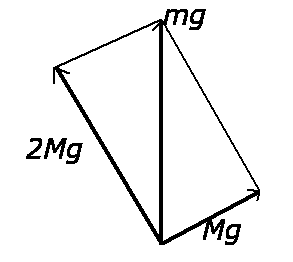
Aufgabe 4: (5 Punkte)
a) Im Gegensatz zur vorherigen Aufgabe herrscht im Seil überall die Spannungskraft 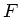 .
Durch die Rolle wird die Kraft lediglich in der Richtung umgelenkt. Daher folgen die Gleichungen
.
Durch die Rolle wird die Kraft lediglich in der Richtung umgelenkt. Daher folgen die Gleichungen
Nach Elimination von 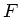 und wegen
und wegen
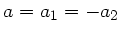 folgt:
folgt:
b) Beim freien Fall ist
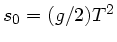 , bei unserer Anordung dagegen
, bei unserer Anordung dagegen
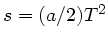 . Bei
. Bei 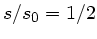 gilt
gilt 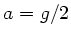 und mit dem Ergebnis von Teil a)
und mit dem Ergebnis von Teil a)
oder
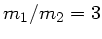 .
.
Harm Fesefeldt
2007-07-31

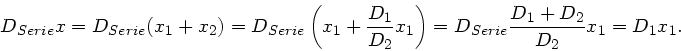
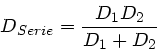
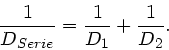

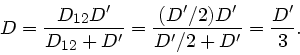
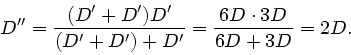
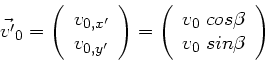
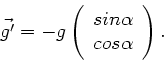

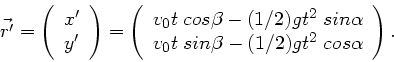
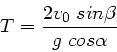
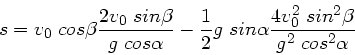
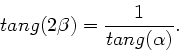

![]() .
Durch die Rolle wird die Kraft lediglich in der Richtung umgelenkt. Daher folgen die Gleichungen
.
Durch die Rolle wird die Kraft lediglich in der Richtung umgelenkt. Daher folgen die Gleichungen