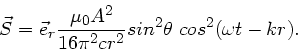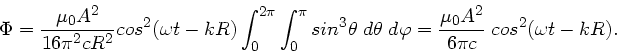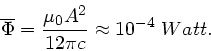Weitere Aufgaben
Aufgabe 1: (7 Punkte)
Zwei elektromagnetische Wellen gleicher Frequenz, aber
unterschiedlicher Phase, breiten sich in der
gleichen Richtung im Raum aus. Unter welchen Umständen
addieren sich die Intensitäten der beiden Wellen so, daß
die Gesamtintensität immer gleich der Summe der Einzelintensitäten
der beiden Wellen ist, und zwar unabhängig von deren Phasenbeziehung ?
Aufgabe 2: (6 Punkte)
Das Strahlungsfeld einer bestimmten Antenne kann approximativ
dargestellt werden durch
wobei
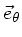 der Polarwinkel- Einheitsvektor und
der Polarwinkel- Einheitsvektor und
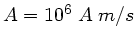 ist.
Wie groß ist der mittlere Energiefluß durch eine Kugeloberfläche mit
Radius
ist.
Wie groß ist der mittlere Energiefluß durch eine Kugeloberfläche mit
Radius 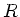 und Kugelmittelpunkt im Mittelpunkt der Antenne ?
und Kugelmittelpunkt im Mittelpunkt der Antenne ?
Lösungen
Aufgabe 1: (7 Punkte)
Wir betrachten zwei elektromagnetische Wellen
Die Überlagerung beider ist
Das Quadrat der Feldstärke berechnet sich zu
Um die Intensität zu erhalten, muß dieser Ausdruck über die Zeit
gemittelt werden. Dieses ergibt
Der letzte Term in diesem Ausdruck soll verschwinden, unabhängig
von der Phase 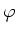 . Das ist nur möglich, wenn
. Das ist nur möglich, wenn
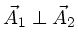 , d.h. die beiden Felder müssen
senkrecht zueinander stehen.
, d.h. die beiden Felder müssen
senkrecht zueinander stehen.
Aufgabe 2: (6 Punkte)
Zunächst muß das Magnetfeld berechnet werden. Im allgemeinen Fall
kann das mit Hilfe der Maxwellschen Gleichung
 gelöst werden. Wir wählen
hier einen anschaulichen Weg. Das Fernfeld des Dipols kann als
ebene Welle betrachtet werden. Für eine solche Welle gilt bei
rechtwinkligen Koordinaten
gelöst werden. Wir wählen
hier einen anschaulichen Weg. Das Fernfeld des Dipols kann als
ebene Welle betrachtet werden. Für eine solche Welle gilt bei
rechtwinkligen Koordinaten
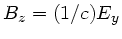 , wenn die Ausbreitungsrichtung
in der
, wenn die Ausbreitungsrichtung
in der 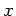 - Achse und das elektrische Feld in Richtung der
- Achse und das elektrische Feld in Richtung der 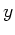 - Achse
liegt. Hier gilt für die Einheitsvektoren
- Achse
liegt. Hier gilt für die Einheitsvektoren
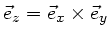 . Entsprechend gilt
für Kugelkoordinaten
. Entsprechend gilt
für Kugelkoordinaten
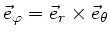 . Das
. Das 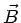 - Feld
liegt also in
- Feld
liegt also in
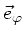 - Richtung und hat den Wert
- Richtung und hat den Wert
Der Energiefluß ist durch den Poynting- Vektor gegeben,
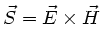 . Da
. Da
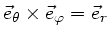 , folgt
, folgt
Diesen Ausdruck müssen wir über die Kugeloberfläche mit Radius
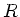 integrieren,
integrieren,
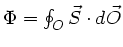 mit
mit
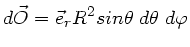 .
Alles eingesetzt, ergibt für den Energiefluß
.
Alles eingesetzt, ergibt für den Energiefluß
Die zeitliche Mittelwertbildung über die Cosinus- Funktion ergibt
einen weiteren Faktor 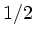 , sodaß schließlich
, sodaß schließlich
Harm Fesefeldt
2007-12-19