Fragen zur Wellengleichung
Frage 1:
a) Welche verschiedenen Wellenformen messen wir bei einem
Erdbeben ?
b) Falls Sie bei Frage a) zwei verschiedene Wellenformen genannt
haben, welche der beiden erreicht uns zuerst ?
c) Welche der beiden Wellenformen kann man auf einem Schiff auf dem
Ozean messen ?
Frage 2:
Von einer punktförmigen Quelle breitet sich isotrop im Raum ein
Wellenpaket aus. Wie könnte Ihrer Meinung nach die allgemeine Form
dieses Wellenpaketes aussehen ? Diskutieren Sie nicht
die allgemeine dreidimensionale Wellengleichung
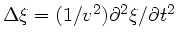 , sondern
raten Sie einen Ansatz und argumentieren mit der Energieerhaltung.
, sondern
raten Sie einen Ansatz und argumentieren mit der Energieerhaltung.
Frage 3:
Warum darf ein Flugzeug nicht über längere Zeit mit
Schallgeschwindikeit fliegen ?
Frage 4:
Drei Lautsprecher senden harmonische Schallwellen gleicher Frequenz
aus. An einem Punkt 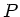 , weit entfernt von den Lautsprechern, haben
die drei Wellen gleiche Amplitude, aber verschiedene Phasen
, weit entfernt von den Lautsprechern, haben
die drei Wellen gleiche Amplitude, aber verschiedene Phasen
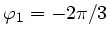 ,
,
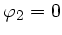 und
und
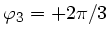 .
Zeigen Sie, daß die Schallintensität am Ort
.
Zeigen Sie, daß die Schallintensität am Ort  zu allen Zeiten
verschwindet.
zu allen Zeiten
verschwindet.
Zur Erinnerung:
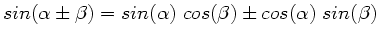 .
.
Frage 5:
Die mittlere quadratische Geschwindigkeit der Moleküle eines
zweiatomigen Gases beträgt bei einem Versuch 461 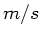 . Wie groß
ist die Schallgeschwindigkeit in diesem Gas ? Zur Erinnerung:
die mittlere quadratische Geschwindigkeit ist (siehe Physik I)
. Wie groß
ist die Schallgeschwindigkeit in diesem Gas ? Zur Erinnerung:
die mittlere quadratische Geschwindigkeit ist (siehe Physik I)
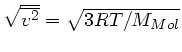 .
.
Lösungen
Frage 1:
a) In festen Stoffen hat man longitudinale und transversale Wellen.
Die Geschwindigkeiten sind
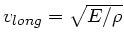 und
und
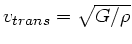 . Zusatzfrage: Was ist
. Zusatzfrage: Was ist 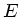 und was ist
und was ist 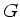 ?
?
b) Da
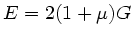 mit
mit 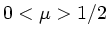 , ist immer
, ist immer 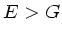 und daher
und daher
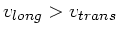 . Die longitudinale Welle erreicht uns zuerst.
. Die longitudinale Welle erreicht uns zuerst.
c) In Wasser und Luft gibt es keine transversalen Wellen, daher messen
wir auf dem Schiff nur longitudinale Wellen.
Frage 2:
Mit der Analogie zur eindimensionalen Wellenfunktion raten wir
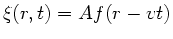 . Wir nehmen das negative Vorzeichen im Argument
der Funktion, da die Ausbreitung in Richtung von wachsendem
. Wir nehmen das negative Vorzeichen im Argument
der Funktion, da die Ausbreitung in Richtung von wachsendem  verläuft. Die Energie in der Kugelschale mit dem Volumen
verläuft. Die Energie in der Kugelschale mit dem Volumen
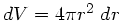 ist
ist
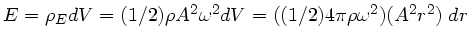 , mit der Amplitude
, mit der Amplitude 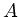 der Welle. Wegen
Energieerhaltung darf diese Energie nicht von
der Welle. Wegen
Energieerhaltung darf diese Energie nicht von 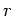 abhängen, daher
muß
abhängen, daher
muß 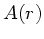 eine Funktion von
eine Funktion von 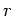 sein, und zwar
sein, und zwar 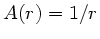 . Die Lösung
ist also
. Die Lösung
ist also
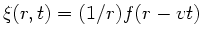 .
.
Frage 3:
Bewegt sich eine Schallquelle mit Schallgeschwindigkeit, so kann sich
von ihr kein Schall ausbreiten. Es entsteht ein Energiestau am Ort
der Schallquelle, der so groß werden kann, daß die Schallquelle
zerstört wird. Es ist deshalb absolut notwendig, beim Übergang zum
Überschall den kritischen Bereich so schnell wie möglich zu
passieren.
Frage 4:
Die Wellen am Orte 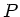 sind
sind
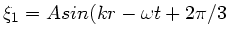 ,
,
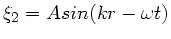 und
und
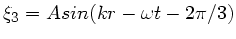 . Die Überlagerung der ersten und dritten Welle ergibt
. Die Überlagerung der ersten und dritten Welle ergibt
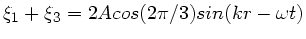 und daher
und daher
![$\xi_{1} + \xi_{2} + \xi_{3} = A [2 cos(2\pi/3) +1] sin(kr - \omega t)$](img29.gif) .
Da
.
Da
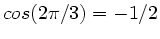 ist, folgt
ist, folgt
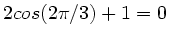 und
und 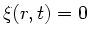 .
.
Frage 5:
Die Schallgeschwindigkeit in einem Gas ist
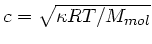 .
Daher folgt
.
Daher folgt
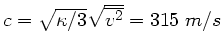 .
.
Harm Fesefeldt
2007-12-04
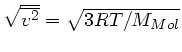 .
.
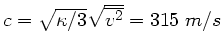 .
.