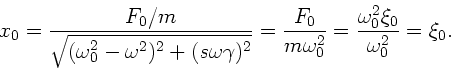Fragen zu harmonischen Schwingungen
Frage 1:
Ein Maximum der Auslenkung einer harmonischen Schwingung
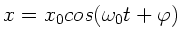 liegt um
liegt um 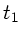 vor dem
Zeitnullpunkt. Wie groß ist der Nullphasenwinkel
vor dem
Zeitnullpunkt. Wie groß ist der Nullphasenwinkel 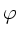 ?
?
Frage 2:
Weshalb treten in der Ort-Zeit- Funktion der harmonischen Schwingung
zwei Integrationskonstanten auf ? Welche physikalische Bedeutung
haben diese beiden Konstanten ?
Frage 3:
Stellen Sie für die Federschwingung in einem Diagramm die potentielle
Energie über der Zeit dar !
Frage 4:
Wie lauten die Differentialgleichung der harmonischen Schwingung und
die Strom-Zeit- Funktion in einem elektrischen Schwingkreis ?
Frage 5:
Zeigen Sie, daß für die gedämpfte Schwingung
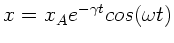 die Beziehung
die Beziehung
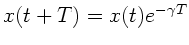 erfüllt ist ?
erfüllt ist ?
Frage 6:
Wie kann man durch Beobachten der Ort-Zeit- Funktion einer
gedämpften Schwingung die Abklingkonstante 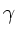 bestimmen ?
bestimmen ?
Frage 7:
Welche Formen der gedämpften Schwingung ergeben sich für
die Fälle
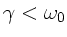 ,
,
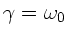 und
und
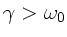 ?
?
Frage 8:
Eine Federschwingung wird durch die Gleitreibung zwischen der
schwingenden Punktmasse und ihrer horizontalen Unterlage gedämpft.
Gilt für diese Bewegung die Ort-Zeit- Funktion
?
Frage 9:
Die Differentialgleichung für die Stromstärke im elektrischen
Schwingkreis lautet
Wie groß sind die Kreisfrequenz 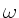 und die Abklingkonstante
und die Abklingkonstante
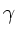 der gedämpften Schwingung ?
der gedämpften Schwingung ?
Frage 10:
Zeigen Sie am Beispiel einer erzwungenen Federschwingung, daß bei
äußerer Erregung für sehr kleine Frequenzen
und beliebige Dämpfungen die Resonatoramplitude mit der
Erregeramplitude übereinstimmt ! Geben Sie hierfür eine
anschauliche Erklärung. Zur Erinnerung: Die DGL
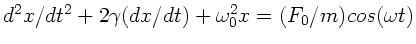 wird gelöst durch
wird gelöst durch
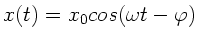 mit
mit
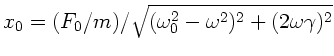 .
.
Frage 11:
Zeigen Sie, daß bei äußerer Erregung und bei beliebiger
Dämpfung die Resonatoramplitude verschwindet, wenn die
Erregerfrequenz sehr groß wird ! Geben Sie hierfür eine
anschauliche Erklärung.
Lösungen:
Frage 1:
Ein Maximum der Auslenkung erhält man, wenn das Argument der
Cosinusfunktion gleich Null wird, daher
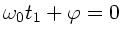 oder
oder
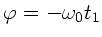 . Da
. Da 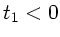 ist, wird
ist, wird
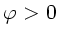 .
.
Frage 2:
Die Ort-Zeit- Funktion der harmonischen Schwingung ist die
Lösung einer DGL, die die zweite Ableitung nach der Zeit enthält.
Bei zweimaliger Integration treten zwei Konstanten auf, und zwar die
Amplitude 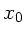 und der Nullphasenwinkel
und der Nullphasenwinkel 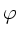 .
.
Frage 3:
Aus
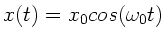 folgt
folgt
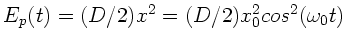 .
.
Frage 4:
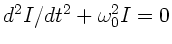 und
und
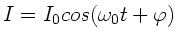 . Die DGL der harmonischen
Schwingung gilt also für den Strom
. Die DGL der harmonischen
Schwingung gilt also für den Strom 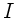 .
.
Frage 5:
Aus
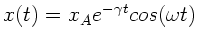 folgt
folgt
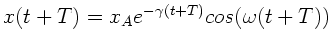 und
und
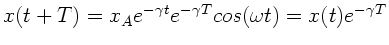 .
.
Frage 6:
Man mißt das Amplitudenverhältnis zweier aufeinanderfolgender
Schwingungen 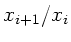 und die Zeitdauer
und die Zeitdauer 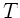 zwischen dem
Auftreten der Amplituden auf ein- und derselben Seite der Auslenkung.
Hierfür gilt
zwischen dem
Auftreten der Amplituden auf ein- und derselben Seite der Auslenkung.
Hierfür gilt
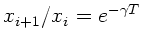 und daher
und daher
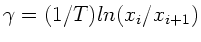 . Man erhält allerdings eine
größere Genauigkeit, wenn man eine größere Anzahl
. Man erhält allerdings eine
größere Genauigkeit, wenn man eine größere Anzahl 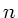 von
Schwingungen abwartet. Dann gilt entsprechend
von
Schwingungen abwartet. Dann gilt entsprechend
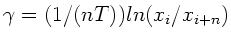 .
.
Frage 7:
Der erste ist der normale Schwingfall, der zweite der aperiodische
Grenzfall und der Dritte der Kriechfall. Zusatzfrage: Worin unterscheidet
sich der Kriechfall vom aperiodischen Grenzfall ?
Frage 8:
Die Gleitreibung hat das Kraftgesetz
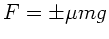 . Daraus folgt
die Bewegungsgleichung
. Daraus folgt
die Bewegungsgleichung
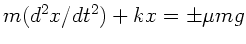 .
Die Lösung dieser Gleichung ist keine harmonische
Schwingung.
.
Die Lösung dieser Gleichung ist keine harmonische
Schwingung.
Frage 9:
Vergleicht man die DGL für den elektrischen Schwingkreis mit
der DGL
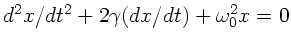 ,
so erhält man sofort
,
so erhält man sofort
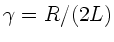 ,
,
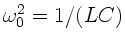 und
und
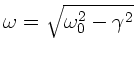 .
.
Frage 10:
Anschaulich ist relativ klar, daß die Feder nicht mehr schwingt,
wenn die Erregerfrequenz gleich Null wird. Die Feder wird vielmehr
wie eine starre Stange mitbewegt. Aus den Formeln ist das allerdings nicht
so einfach zu schließen. Das eine freie Ende der Feder wird mit der
Auslenkung
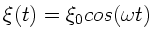 bewegt. Die Federkraft
ist dann
bewegt. Die Federkraft
ist dann
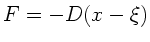 , wenn
, wenn 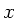 die Dehnung der Feder aus der
Ruhelage ist. Die Bewegungsgleichung folgt hieraus zu
die Dehnung der Feder aus der
Ruhelage ist. Die Bewegungsgleichung folgt hieraus zu
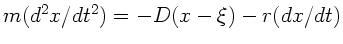 oder
oder
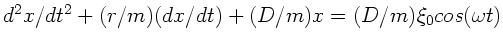 .
Vergleich mit der allgemeinen Schwingungsgleichung
.
Vergleich mit der allgemeinen Schwingungsgleichung
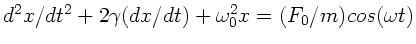 zeigt, daß
zeigt, daß
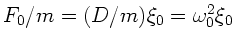 sein muß. Daher folgt für
sein muß. Daher folgt für 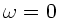 :
:
Frage 11:
Setzt man in die Formel für 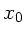 die Erregerfrequenz
die Erregerfrequenz
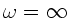 ein, so folgt
ein, so folgt 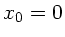 . Die Feder kann die
Punktmasse nicht mehr bewegen, weil bei endlich großen Auslenkungen die
Beschleunigung unendlich groß wäre und dazu eine unendlich große
Kraft erforderlich wäre.
. Die Feder kann die
Punktmasse nicht mehr bewegen, weil bei endlich großen Auslenkungen die
Beschleunigung unendlich groß wäre und dazu eine unendlich große
Kraft erforderlich wäre.
Harm Fesefeldt
2007-11-28
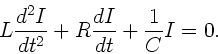
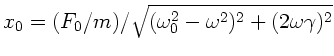 .
.
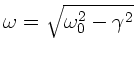 .
.