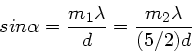Übung Nr. 12
Abgabetermin: Mittwoch, den 30. Januar 2001
Aufgabe 1: (6 Punkte)
Die Gangdifferenz zwischen dem ersten an der Oberseite und dem ersten
an der Unterseite reflektierten Strahl beträgt
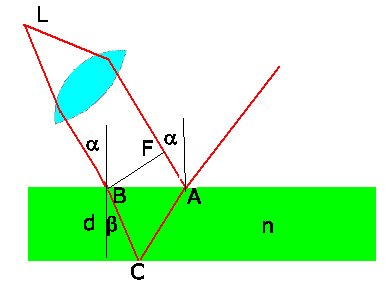
Hierfür können wir auch schreiben
Mit
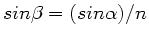 und
und
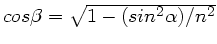 folgt:
folgt:
Dieses kann man umformen zu
Man erhält Auslöschung, wenn diese Gangdifferenz gleich
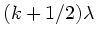 mit ganzer Zahl
mit ganzer Zahl 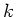 ist. Also folgt
ist. Also folgt
Aufgabe 2: (7 Punkte)
a) Die Intensitätsverteilung am unendlich langen Einzelspalt ist nach
Vorlesung
mit
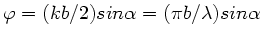 . Extremwerte
ergeben sich für
. Extremwerte
ergeben sich für
Minima ergeben sich für
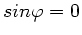 und
und
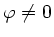 , d.h.
, d.h.
Maxima erhält man entsprechend für
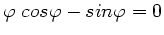 oder
oder
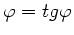 .
Dieses wird erfüllt durch
.
Dieses wird erfüllt durch
Die Maxima liegen also nicht exakt zwischen den Minima, sondern
geringfügig zu kleineren Winkeln verschoben. Wir können das noch durch
die wahren Ablenkwinkel ausdrücken. Wegen
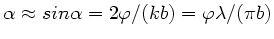 folgt für die Minima
folgt für die Minima
und für die ersten drei Nebenmaxima:
b) Wie wir in Teil a) gesehen haben, liegen die Maxima zwar nicht exakt
zwischen den Minima, sind aber nur geringfügig verschoben. Zur
Berechnung der Intensität in den Maxima können wir daher setzen
Dann ist aber
 und daher
und daher
c) Die Intensität des Hauptmaximums fällt auf die Hälfte ihres
Wertes ab, wenn
oder
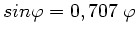 . Diese Gleichung wird gelöst durch
. Diese Gleichung wird gelöst durch
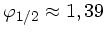 . Da
. Da
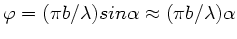 , folgt
, folgt
und
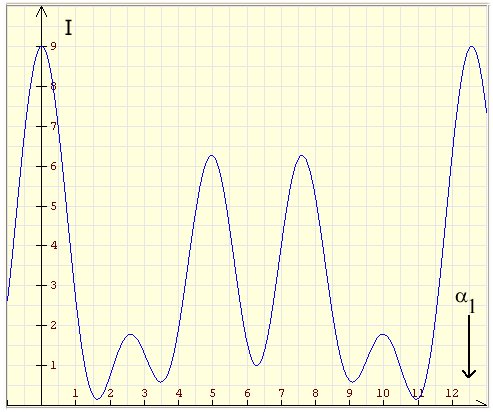
Aufgabe 3: (7 Punkte)
Die Feldstärke der drei Wellen kann geschrieben werden als (siehe Skript)
Die Intensität ist
Ausmultiplizieren und mit Hilfe der Formel
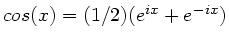 folgt
folgt
Die Hauptmaximam liegen bei den Winkeln, bei denen die Phasen aller drei
Teilwellen übereinstimmen. Bezeichnen wir den Wegunterschied der zweiten und
dritten Welle gegeüber der ersten mit 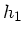 und
und 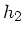 , so ist
, so ist
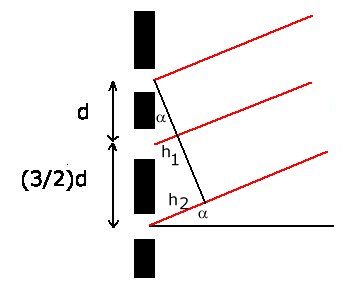
Da 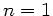 , ist der Wegunterschied identisch mit dem optischen Gangunterschied.
Maximale Verstärkung erhalten wir, wenn gleichzeitig
, ist der Wegunterschied identisch mit dem optischen Gangunterschied.
Maximale Verstärkung erhalten wir, wenn gleichzeitig
wobei 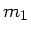 und
und 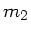 ganze Zahlen sind. Dieses kann nur dann gleichzeitig
erfüllt werden, wenn
ganze Zahlen sind. Dieses kann nur dann gleichzeitig
erfüllt werden, wenn
gilt, d.h.
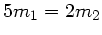 . Die einfachste, von Null verschiedene
Lösung ist
. Die einfachste, von Null verschiedene
Lösung ist 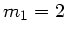 und
und 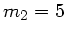 . Das erste Hauptmaximum liegt also
unter dem Winkel
. Das erste Hauptmaximum liegt also
unter dem Winkel
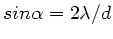 oder
oder 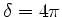 . Allgemein
gilt:
. Allgemein
gilt:
Für die Intensitäten in den Maxima gilt
Einem Winkel von
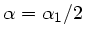 entsprecht
entsprecht 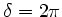 .
Hierfür erhalten wir:
.
Hierfür erhalten wir:
und
Harm Fesefeldt
2008-01-11
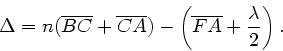

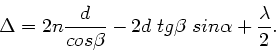
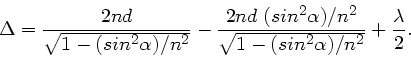
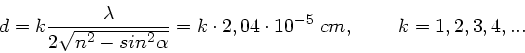
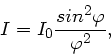
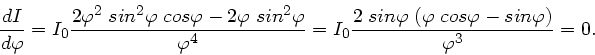
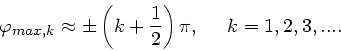
![\begin{displaymath}
I_{max,k} = \frac{I_{0}}{\varphi^{2}_{max,k}} = \frac{I_{0}}
{[(k+1/2)\pi]^{2}}
\end{displaymath}](img36.gif)
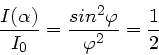
![\begin{displaymath}
I(\delta) = C^{2} \left[ 3 + 2 \; cos(\delta) + 2 \; cos\lef...
...a
\right) + 2 \; cos \left( \frac{5}{2}\delta \right) \right].
\end{displaymath}](img46.gif)
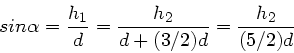

![]() , ist der Wegunterschied identisch mit dem optischen Gangunterschied.
Maximale Verstärkung erhalten wir, wenn gleichzeitig
, ist der Wegunterschied identisch mit dem optischen Gangunterschied.
Maximale Verstärkung erhalten wir, wenn gleichzeitig