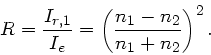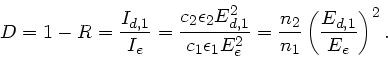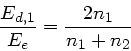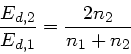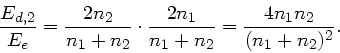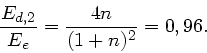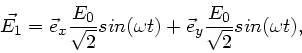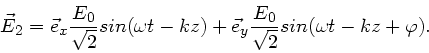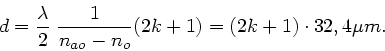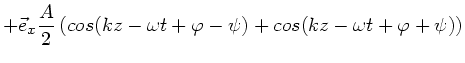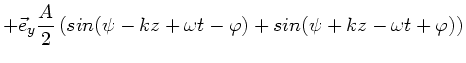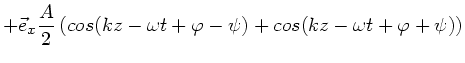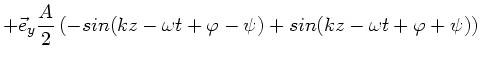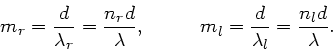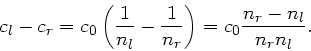Lösungsvorschläge zur Übung Nr. 11
Besprechung: Mittwoch, den 24. Januar 2001
Aufgabe 1: (6 Punkte)
Der Brechungsindex der Glasscheibe sei 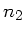 , der Brechungsindex
der umgebenden Luft
, der Brechungsindex
der umgebenden Luft  . Für das reflektierte elektrische
Feld vor der Glasplatte gilt nach Vorlesung
. Für das reflektierte elektrische
Feld vor der Glasplatte gilt nach Vorlesung
wenn 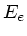 die Feldtärke des einfallenden Lichtes ist. Für die
reflektierte Intensität gilt
die Feldtärke des einfallenden Lichtes ist. Für die
reflektierte Intensität gilt
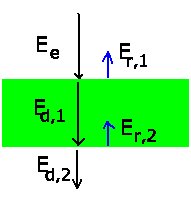
Wegen Energieerhaltung folgt für die durchgelassene Intensität
Daraus folgt
Bei unserer Ableitung gilt diese Formel zunächst nur für die
Beträge der Feldstärken. Wir wissen aber, daß die durchgelassenen
Komponenten keinen Phasensprung haben, also muß diese Formel auch
für das Vorzeichen gelten. Bei der zweiten Grenzschicht erhalten
wir entsprechend mit Vertauschung von 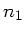 und
und 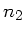 :
:
und daher
Setzen wir jetzt noch 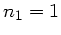 und
und 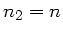 , so erhalten wir
, so erhalten wir
Aufgabe 2: (7 Punkte)
Wir legen die 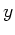 -Achse in Richtung der optischen Achse, dann können
wir die lineare Welle darstellen durch
-Achse in Richtung der optischen Achse, dann können
wir die lineare Welle darstellen durch
wobei wir ersichtlich noch den Nullpunkt der 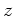 -Achse in die vordere
Ebene des Quarzplättchens gelegt haben. Nach Durchgang durch das
Plättchen hat die Komponente in
-Achse in die vordere
Ebene des Quarzplättchens gelegt haben. Nach Durchgang durch das
Plättchen hat die Komponente in 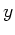 -Richtung eine Phasendifferenz
von
-Richtung eine Phasendifferenz
von
gegenüber der Komponente in 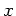 -Richtung (siehe Vorlesung).
Daher können wir schreiben
-Richtung (siehe Vorlesung).
Daher können wir schreiben
Diese Welle ist im allgemeinen elliptisch (zirkular) polarisiert,
nur für
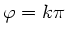 mit
mit 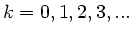 ist sie linear polarisiert.
Während man für
ist sie linear polarisiert.
Während man für 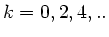 keine Änderung der Polarisationsebene
erhält, ergibt sich für
keine Änderung der Polarisationsebene
erhält, ergibt sich für 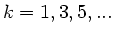 eine Drehung der Ebene um
eine Drehung der Ebene um
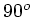 . Wir folgern also, daß
. Wir folgern also, daß
sein muß, mit 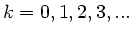 Aufgelöst nach der Dicke
Aufgelöst nach der Dicke 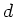 folgt:
folgt:
Aufgabe 3: (7 Punkte)
Zur Übung zeigen wir zunächst einmal, daß die Summe einer linkszirkular
polarisierten und rechtszirkular polarisierten Welle gleicher Amplitude
eine linear polarisierte Welle ergibt. Es sei also
Die Umformung der Summe
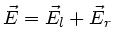 in eine
linear polarisierte Welle ist außerordentlich mühsam. Wir machen daher
den allgemeinen Ansatz einer linearen Welle,
in eine
linear polarisierte Welle ist außerordentlich mühsam. Wir machen daher
den allgemeinen Ansatz einer linearen Welle,
wobei 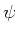 und die Phase
und die Phase 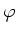 zunächst unbekannt sind. Der Ausdruck
in der vorderen Klammer ist ein belibiger, aber konstanter Vektor in der
zunächst unbekannt sind. Der Ausdruck
in der vorderen Klammer ist ein belibiger, aber konstanter Vektor in der
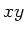 - Ebene. Diese Welle läßt sich umformen zu
- Ebene. Diese Welle läßt sich umformen zu
Diesen Ausdruck vergleichen wir mit der Summe der zirkular polarisierten
Wellen
und erhalten 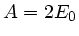 ,
,
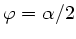 und
und
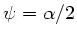 .
Wir können daher allgemein schreiben:
.
Wir können daher allgemein schreiben:
Wir sehen also, daß bei einer Phasendifferenz von 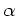 der zirkular
polarisierten Wellen eine Drehung der Polarisationsebene der linear
polarisierten Welle von
der zirkular
polarisierten Wellen eine Drehung der Polarisationsebene der linear
polarisierten Welle von 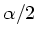 stattgefunden hat.
stattgefunden hat.
Die Zahl der Umläufe der zirkular polariserten Wellen auf der Strecke
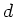 ist:
ist:
Die Differenz der Drehwinkel ist also
wobei 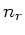 und
und 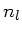 die Brechungsindizes sind. Die Drehung der
Polarisationsebene der linear polarisierten Welle ist daher (siehe oben)
die Brechungsindizes sind. Die Drehung der
Polarisationsebene der linear polarisierten Welle ist daher (siehe oben)
Daraus folgt
Für die Differenz der Phasengeschwindigkeiten erhalten wir
Da die Differenz der Brechungsindizes sehr klein ist, darf man im Nenner
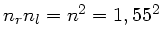 approximieren und erhält
approximieren und erhält
Im Vergleich zur Lichtgeschwindigkeit ist dieser Unterschied wirklich
verschwindend klein.
Harm Fesefeldt
2008-01-02