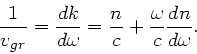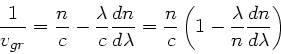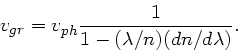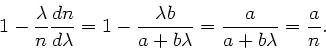Lösungsvorschläge zur Übung Nr. 9
(Bonusübung)
Besprechung: Mittwoch, den 17. Januar 2001
Aufgabe 1:(Bonusaufgabe) (5 Punkte)
Diese Näherung kommt aus der allgemeinen Formel
wenn man nur eine Resonanz aus der Summe herausgreift und den Beitrag aller
anderen Resonanzen in der Konstanten 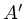 zusammenfasst:
zusammenfasst:
Zur Vereinfachung wird die Wurzel noch entwickelt:
Auch die Konstanten 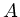 und
und 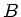 hängen natürlich noch schwach von
hängen natürlich noch schwach von
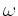 ab, was wir aber hier vernachlässigen.
Der Brechungsindex ist als Funktion der Frequenz gegeben. Für die
Phasengeschwindigkeit folgt:
ab, was wir aber hier vernachlässigen.
Der Brechungsindex ist als Funktion der Frequenz gegeben. Für die
Phasengeschwindigkeit folgt:
Zur Berechnung der Gruppengeschwindigkeit schreiben wir zunächst
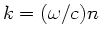 und bedenken, daß
und bedenken, daß 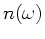 noch ein Funktion
von
noch ein Funktion
von 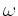 ist. Daher gilt
ist. Daher gilt
Auswertung dieser Formel ergibt
und daher
Zur Anfertigung der Skizze bemerken wir zunächst, daß für
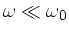 und
und
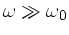 die folgenden
Grenzwerte angenommen werden:
die folgenden
Grenzwerte angenommen werden:
Bei den Skizzen muß beachtet werden, daß unsere Formel auf
der Resonanz selbst nicht gilt. Der Brechungsindex und die
Phasengeschwindigkeit dürfen natürlich nicht kleiner
Null werden.
Aufgabe 2:(Bonusaufgabe) (5 Punkte)
a) Die Intensität ist proportional zu 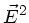 . Für die elektrische
Feldstärke machen wir den Ansatz
. Für die elektrische
Feldstärke machen wir den Ansatz
wobei die Wellenzahl 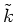 komplex ist, da der Brechungsindex
komplex ist, da der Brechungsindex
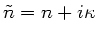 komplex ist (siehe Skript).
Da
komplex ist (siehe Skript).
Da
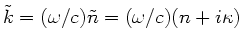 , können
wir die elektrische Feldstärke schreiben:
, können
wir die elektrische Feldstärke schreiben:
Daraus folgt für die Intensität
Die Intensität ist also bei der Strecke
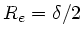 auf den
auf den
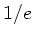 -ten Teil abgesunken.
-ten Teil abgesunken.
b) Das Magnetfeld 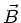 ist nach Maxwell in der folgenden Form an die
elektrische Feldstärke gekoppelt:
ist nach Maxwell in der folgenden Form an die
elektrische Feldstärke gekoppelt:
Hier ist aber jetzt 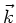 auch komplex. Wir schreiben daher
auch komplex. Wir schreiben daher
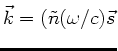 mit dem Einheitsvektor
mit dem Einheitsvektor 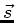 in Ausbreitungsrichtung. Mit
in Ausbreitungsrichtung. Mit
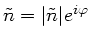 und
und
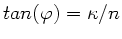 folgt
folgt
Der Phasenwinkel ist also
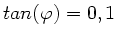 oder
oder
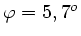 .
.
Aufgabe 3:(Bonusaufgabe) (5 Punkte)
Wir hatten bereits in Aufgabe 1 die Formel
Wegen
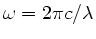 folgt
folgt
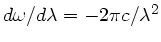 und daher
und daher
Dieses kann man auch schreiben:
Hierbei ist also jetzt 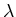 die Wellenlänge im Vakuum. Die Phasengeschwindigkeit
ist
die Wellenlänge im Vakuum. Die Phasengeschwindigkeit
ist 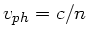 und
und
Daher ist
unabhängig von der Wellenlänge im Vakuum.
b) Die Gruppengeschwindigkeit muß kleiner als die Vakuumlichtgeschwindigkeit sein,
daher muß 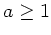 sein.
sein.
Harm Fesefeldt
2008-01-02
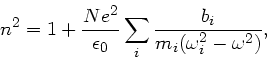
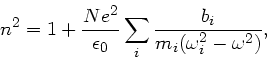
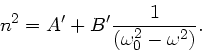
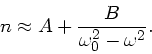
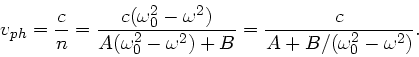
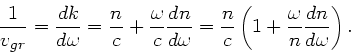
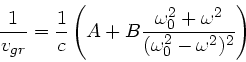
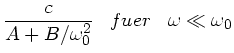
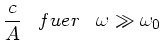
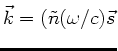 mit dem Einheitsvektor
mit dem Einheitsvektor