Lösungsvorschläge zur Übung Nr. 3
Besprechung: Mittwoch, den 15. November 2000
Aufgabe 1: (8 Punkte)
Der Strom bzw die Spannung als Funktion der Zeit ist in der folgenden
Abbildung gegeben,
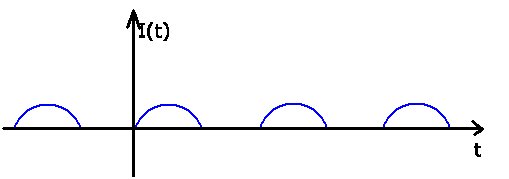
Wir diskutieren zunächst die Entwicklung
Mit
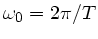 und
und
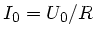 sind die Amplituden
sind die Amplituden
Zur Lösung der Integrale schreiben wir zunächst mit Hilfe der beiden
Formeln
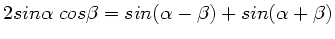 und
und
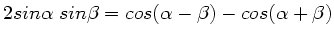 :
:
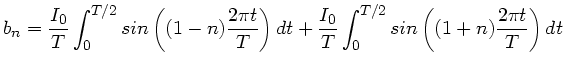 |
|
|
|
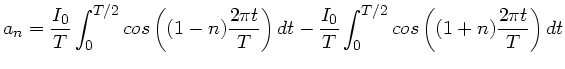 |
|
|
(2) |
Diese Integrale sind zwar mühsam, aber elementar lösbar und ergeben:
Der Strom läßt sich also schreiben:
b) Zur Bestimmung der Phasendifferenzen der Oberschwingungen gegenüber
der Grundschwingung entwickeln wir gemäß
und erhalten für 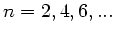 :
:
daher
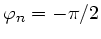 .
.
Aufgabe 2: (8 Punkte)
Wir berechnen die Fourierkoeffizienten
Für 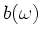 erhalten wir weiter
erhalten wir weiter
In unserem Fall ist 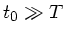 und daher
und daher
Daher gilt die Abschätzung:
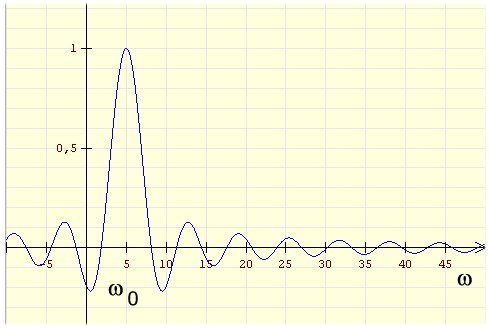
Was bleibt, ist
Diese Funktion hat ein Maximum bei
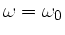 . Für uns interessant
sind die ersten beiden Nullstellen, wir bezeichnen sie mit
. Für uns interessant
sind die ersten beiden Nullstellen, wir bezeichnen sie mit
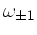 :
:
Die Frequenzbreite ist also ungefähr
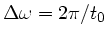 oder
oder
Der Sender sendet also mit der Frequenz
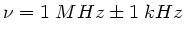 .
.
Aufgabe 3: (4 Punkte)
Die Schallgeschwindigkeit ist
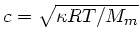 , daher
, daher
Die Wellenlänge hängt bei stehenden Wellen nicht von der Temperatur ab,
daher können wir schreiben
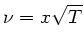 und
und
Integration dieser DGL liefert
wobei 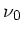 die Frequenz bei der Temperatur
die Frequenz bei der Temperatur
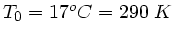 ist. Mit
ist. Mit
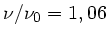 folgt
folgt
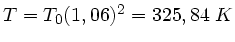 und
und
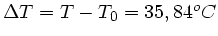 .
.
Aufgabe 4: (10 Punkte)
a) Der S trom 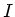 ist gegeben durch
ist gegeben durch
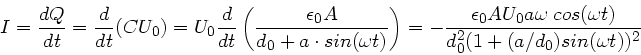 |
(3) |
b) Spezielle Lösung:
Man könnte die Amplituden des Grundtones und des ersten Obertones
mit der Integraldefinition der Fourierkoeffizienten berechnen. Dieses
Vorgehen erweist sich allerdings in diesem Fall bereits als
außerordentlich schwierig. Da nach Hinweis 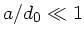 ist,
können wir nach Potenzen von
ist,
können wir nach Potenzen von
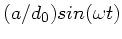 entwickeln. Wegen
entwickeln. Wegen
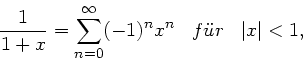 |
(4) |
folgt in zweiter Ordnung von 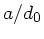 :
:
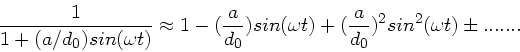 |
(5) |
und
Das Verhältnis der Amplituden ist
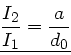 |
(9) |
Die Reihenentwicklung zu dieser Lösung wurde im übrigen in den
Rechenübungen am 4.11.92 auf Seite 3 angegeben.
Allgemeine Lösung:
Die allgemeine Lösung zu dieser Aufgabe wurde ebenfalls in den
Rechenübungen am 4.11.92 diskutiert (Seite 2/3). In der Aufgabe 3
dieser Rechenübungen setzen wir
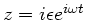 und
entwickeln die Potenzreihe gemäß:
und
entwickeln die Potenzreihe gemäß:
Andererseits erhalten wir für die linke Seite der letzten Gleichung,
wobei wir mit dem konjugiert Komplexen des Nenners erweitern:
Vergleich der Imaginärteile führt auf
Wir setzen
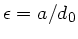 und bemerken, daß nach Aufgabenstellung
und bemerken, daß nach Aufgabenstellung
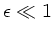 , also erst recht
, also erst recht
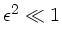 . Daher können
wir im Nenner der linken Seite
. Daher können
wir im Nenner der linken Seite 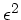 durch
durch
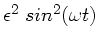 und
und
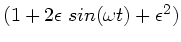 durch
durch
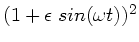 ersetzen. Die Summe auf der
rechten Seite schreiben wir zusätzlich in allgemeiner Form. Dieses
ergibt schließlich für den Strom:
ersetzen. Die Summe auf der
rechten Seite schreiben wir zusätzlich in allgemeiner Form. Dieses
ergibt schließlich für den Strom:
![\begin{displaymath}
I = -\frac{\epsilon_{0} A U_{0} a \omega}{d_{0}^{2}}
\left[ ...
...left( \frac{a}{d_{0}} \right)^{2n-1} sin(2n\omega t) \right] .
\end{displaymath}](img76.gif) |
(10) |
Für das Verhältnis der Amplituden des 1. Obertones zum Grundton erhält
man das gleiche Ergebnis wie in der obigen speziellen Lösung.
Harm Fesefeldt
2007-12-11


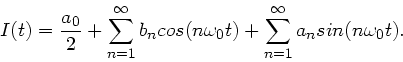
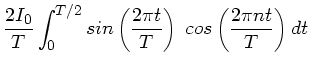
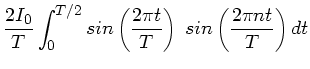
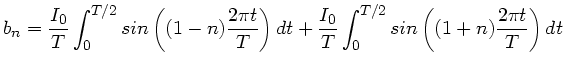
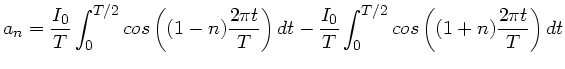
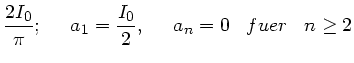
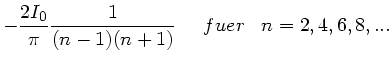
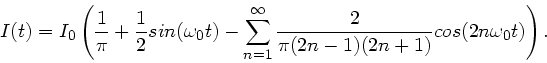
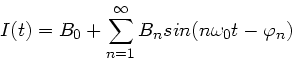
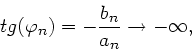
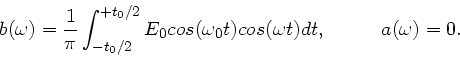
![$\displaystyle \frac{E_{0}}{\pi} \int_{-t_{0}/2}^{+t_{0}/2} \frac{1}{2}
[ cos(\omega_{0} - \omega )t + cos(\omega_{0} + \omega )t ] dt$](img25.gif)
![$\displaystyle \frac{E_{0}}{2\pi} \left[ \frac{sin(\omega_{0}+\omega)t}{\omega_{...
... \frac{sin(\omega_{0}-\omega)t}{\omega_{0}-\omega}
\right]_{-t_{0}/2}^{t_{0}/2}$](img26.gif)
![$\displaystyle \frac{E_{0}t_{0}}{2 \pi} \left( \frac{sin[(\omega_{0}+\omega)(t_{...
...frac{sin[(\omega_{0}-\omega)(t_{0}/2)]}
{(\omega_{0}-\omega)(t_{0}/2)} \right).$](img27.gif)
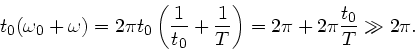
![\begin{displaymath}
\frac{sin[(\omega_{0}+\omega)(t_{0}/2)]}{(\omega_{0}+\omega)(t_{0}/2)}
\approx 0.
\end{displaymath}](img30.gif)

![\begin{displaymath}
b(\omega) = \frac{E_{0}t_{0}}{2 \pi} \frac{sin[(\omega_{0}-\omega)(t_{0}/2)]}
{(\omega_{0}-\omega)(t_{0}/2)}
\end{displaymath}](img31.gif)
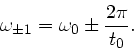
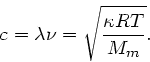
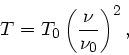
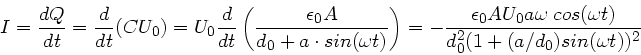
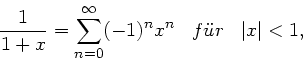
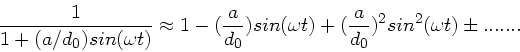
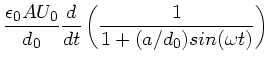
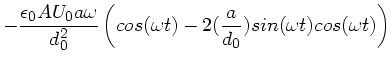
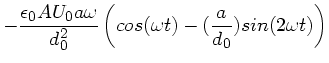
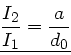
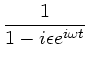
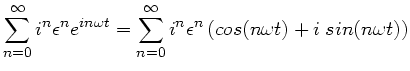
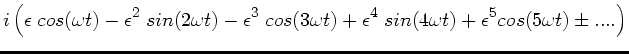
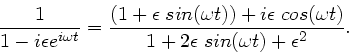
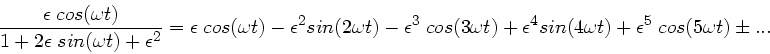
![\begin{displaymath}
I = -\frac{\epsilon_{0} A U_{0} a \omega}{d_{0}^{2}}
\left[ ...
...left( \frac{a}{d_{0}} \right)^{2n-1} sin(2n\omega t) \right] .
\end{displaymath}](img76.gif)