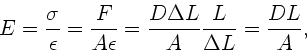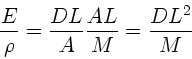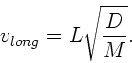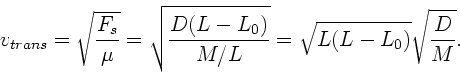Lösungsvorschläge zur Übung Nr. 1
Besprechung: Mittwoch, den 15. November 2000
Aufgabe 1: (5 Punkte)
Bei dieser Aufgabe führen viele Wege zur Lösung. Wir diskutieren
hier 3 Lösungswege.
a) Spezielle Lösung mit trigonometrischen Formeln:
Wir benutzen die einfache trigonometrische Formel
Die Überlagerung läßt sich dann schreiben als
oder
Dieser Ausdruck ergibt sicher eine harmonische Welle der Form
falls
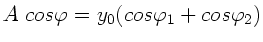 und
und
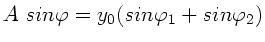 .
Mit den gegebenen Werten für
.
Mit den gegebenen Werten für 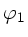 und
und 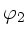 gilt
gilt
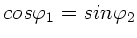 und
und
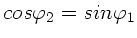 ,
und damit auch
,
und damit auch
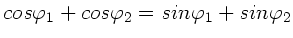 . Vergleich mit den obigen Formeln ergibt also
. Vergleich mit den obigen Formeln ergibt also
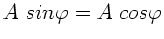 und
und
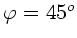 .
Entsprechend finden wir für die Amplitude:
.
Entsprechend finden wir für die Amplitude:
b) Allgemeine Lösung mit trigonometrischen Formeln.
Falls jemand die kompliziertere Formel
gefunden hat, so erhält er die allgemeinere Lösung für die Summe
Dieses ist eine harmonische Welle mit der Phase und Amplitude
Einsetzen der Zahlenwerte ergibt die gleichen Ergebnisse wie in Teil a).
Mit dieser Herleitung sieht man aber, daß die Überlagerung zweier
harmonischer Wellen mit gleicher Amplitude, Frequenz und Wellenlänge
immer eine harmonische Welle ergibt, unabhängig von den Phasen
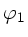 und
und 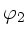 der Einzelwellen. Mit der einfachen
Formel von Lösung a) läßt sich dieser Sachverhalt nicht so einfach
zeigen.
der Einzelwellen. Mit der einfachen
Formel von Lösung a) läßt sich dieser Sachverhalt nicht so einfach
zeigen.
c) Lösung mit komplexen Zahlen:
In Zukunft werden wir in den Lösungsvorschlägen immer mit komplexen
Zahlen arbeiten. Die gegebenen harmonischen Wellen lassen sich darstellen
als Realteil der komplexen Zahlen
Die Überlagerung der zwei harmonischen Wellen mit Phasen 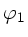 und
und 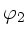 ist dann
ist dann
Auf Grund der allgemeinen Beziehung
folgt in unserem speziellen Fall
mit dem Realteil
Die weitere Argumentation ist die gleiche wie in Teil b).
Aufgabe 2: (6 Punkte)
a) Wir schreiben die Wellenfunktionen als 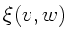 mit
mit 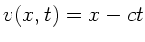 und
und 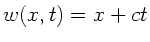 . Dann ergeben sich die ersten partiellen Ableitungen nach
. Dann ergeben sich die ersten partiellen Ableitungen nach
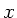 und
und 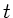 :
:
Da
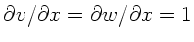 ,
,
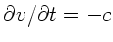 und
und
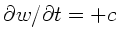 ist,
folgt auch
ist,
folgt auch
Hieraus erhalten wir für die zweiten Ableitungen:
Hierbei wurde (wie immer in der Physik) angenommen, daß die gemischten
partiellen Ableitungen vertauschbar sind. Einsetzen in die Wellengleichung
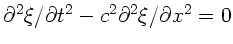 ergibt dann die einfachere Wellengleichung in den Variablen
ergibt dann die einfachere Wellengleichung in den Variablen 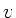 und
und 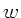 :
:
b) Aus
folgt
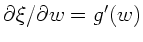 und
und
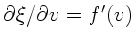 . Diese Bedingungen sind nur
erfüllbar, wenn
. Diese Bedingungen sind nur
erfüllbar, wenn
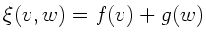 .
.
Aufgabe 3: (4 Punkte)
Das Seil habe die Länge  und Masse
und Masse 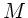 . Dann ist die lineare Massendichte
. Dann ist die lineare Massendichte
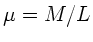 . Wir führen ein Koordinatensystem ein, in dem
. Wir führen ein Koordinatensystem ein, in dem 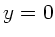 am unteren
Ende des Seils ist:
am unteren
Ende des Seils ist:
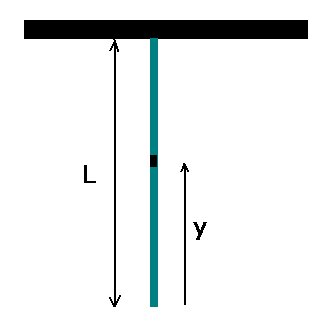
Die Zugkraft auf das Seil am Punkt 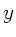 ist
ist
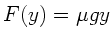 .
Die Phasengeschwindigkeit in diesem Punkt ist
.
Die Phasengeschwindigkeit in diesem Punkt ist
Wir haben also das interessante Ergebnis herausbekommen, daß die
Phasengeschwindigkeit nicht mehr von der linearen Massendichte abhängt,
sondern nur noch von der Koordinate 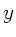 . Die Zeit für den Hin- und
Rücklauf beträgt dann:
. Die Zeit für den Hin- und
Rücklauf beträgt dann:
Einsetzen der Zahlenwerte liefert 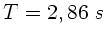 .
.
Aufgabe 4: (5 Punkte)
a) Im Gegensatz zu unseren sonstigen Annahmen muß die Feder in dieser Aufgabe
eine Masse haben, da sich sonst eine Welle nicht fortpflanzen kann.
Die Phasengeschwindigkeit für Longitudinalwellen in der Feder kann völlig
analog zu den Longitudinalwellen in einem Stab hergeleitet werden (siehe
Skript Seite 13 ff). Für diesen gilt
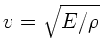 mit dem
Elastizitätsmodul
mit dem
Elastizitätsmodul 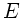 und Dichte
und Dichte 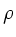 . Der Elastizitätsmodul ist bei
der Feder defininiert durch
. Der Elastizitätsmodul ist bei
der Feder defininiert durch
wobei 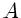 der Querschnitt der Feder bei der Länge
der Querschnitt der Feder bei der Länge 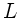 und
und 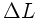 eine kleine Längenausdehnung ist. Mit der Dichte
eine kleine Längenausdehnung ist. Mit der Dichte 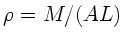 folgt
folgt
und
b) Bei den transversalen Wellen kann man wie bei transversalen Wellen
auf einer Saite vorgehen.
Hierzu bemerken wir, daß die Spannungskraft in der Feder durch
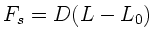 gegeben ist. Daraus folgt sofort:
gegeben ist. Daraus folgt sofort:
b) Für 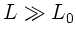 werden beide Geschwindigkeiten gleich. Allerdings
muß in diesem Fall bezweifelt werden, daß in der Feder das Hooksche
Gesetz noch gilt.
werden beide Geschwindigkeiten gleich. Allerdings
muß in diesem Fall bezweifelt werden, daß in der Feder das Hooksche
Gesetz noch gilt.
Harm Fesefeldt
2007-11-28
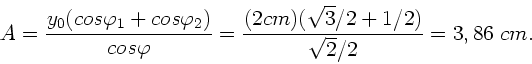
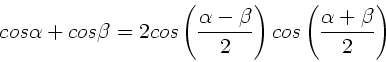
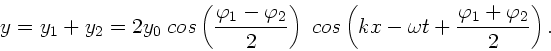
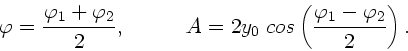
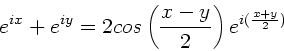
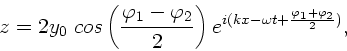
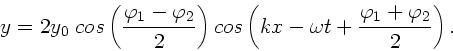

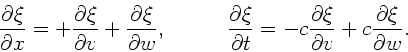
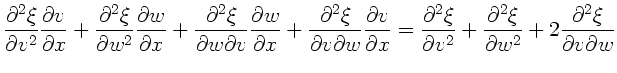
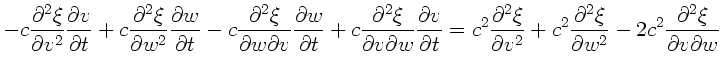
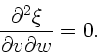


![]() ist
ist
![]() .
Die Phasengeschwindigkeit in diesem Punkt ist
.
Die Phasengeschwindigkeit in diesem Punkt ist
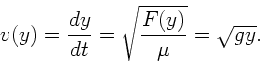
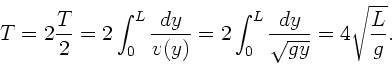
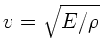 mit dem
Elastizitätsmodul
mit dem
Elastizitätsmodul