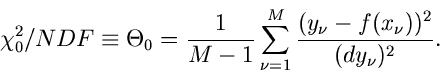Bestimmung von Parametern
Die Maximum Likelihood Methode
Gegeben sei eine zufällige Veränderliche 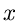 mit der Dichtefunktion
mit der Dichtefunktion
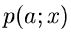 .
. 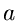 sei ein zunächst unbekannter Parameter der Dichtefunktion.
Die Veränderliche
sei ein zunächst unbekannter Parameter der Dichtefunktion.
Die Veränderliche 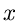 sei das Ergebnis eines Versuches oder einer
Simulation. Wir führen den Versuch (Simulation)
sei das Ergebnis eines Versuches oder einer
Simulation. Wir führen den Versuch (Simulation) 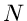 -mal durch und erhalten
-mal durch und erhalten
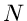 Meßergebnisse
Meßergebnisse
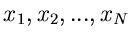 der Veränderlichen
der Veränderlichen 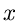 . Unsere
Aufgabe ist jetzt, aus diesen
. Unsere
Aufgabe ist jetzt, aus diesen 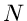 Werten den Parameter
Werten den Parameter 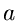 zu bestimmen,
und zwar mit Hilfe einer Schätzfunktion
zu bestimmen,
und zwar mit Hilfe einer Schätzfunktion
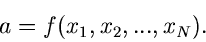 |
(1) |
Im Hinblick auf spätere Anwendungen ist es günstiger, diese Funktion in
impliziter Form zu schreiben:
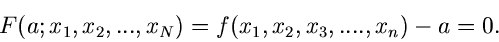 |
(2) |
Die Meßergebnisse
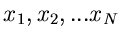 nennen wir eine Stichprobe aus der
Menge der Veränderlichen
nennen wir eine Stichprobe aus der
Menge der Veränderlichen 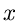 . Der mit Hilfe der Gleichung (1) oder
(2) bestimmte Parameter
. Der mit Hilfe der Gleichung (1) oder
(2) bestimmte Parameter 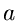 ist nun wieder eine zufällige Veränderliche,
da er aus endlich vielen zufälligen Veränderlichen berechnet wurde.
Der Parameter
ist nun wieder eine zufällige Veränderliche,
da er aus endlich vielen zufälligen Veränderlichen berechnet wurde.
Der Parameter 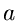 besitzt also eine Dichtefunktion, die wir im folgenden
mit
besitzt also eine Dichtefunktion, die wir im folgenden
mit 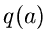 bezeichnen werden. Die Veränderlichen
bezeichnen werden. Die Veränderlichen
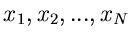 sind unabhängige Veränderliche, da sie aus der mehrmaligen Wiederholung
ein und desselben Versuches erhalten wurden. Wir können daher
sind unabhängige Veränderliche, da sie aus der mehrmaligen Wiederholung
ein und desselben Versuches erhalten wurden. Wir können daher
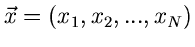 als Vektor auffassen, mit der
Dichtefunktion
als Vektor auffassen, mit der
Dichtefunktion
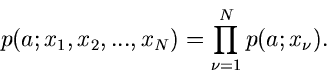 |
(3) |
Für eine Summe 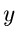 von unabhängigen Veränderlichen,
von unabhängigen Veränderlichen,
hatten wir bereits gezeigt, daß 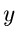 näherungsweise normalverteilt war,
zumindest für große
näherungsweise normalverteilt war,
zumindest für große 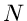 . Dieses Ergebnis kann man verallgemeinern.
Für nicht zu exotische Funktionen
. Dieses Ergebnis kann man verallgemeinern.
Für nicht zu exotische Funktionen
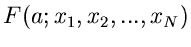 ist
ist 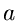 ebenfalls näherungsweise normalverteilt.
Wir dürfen daher davon ausgehen, daß
ebenfalls näherungsweise normalverteilt.
Wir dürfen daher davon ausgehen, daß 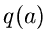 durch einen Erwartungswert
durch einen Erwartungswert
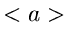 und Varianz
und Varianz 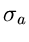 vollständig beschrieben werden kann.
Das Problem ist dann, eine Funktion
vollständig beschrieben werden kann.
Das Problem ist dann, eine Funktion
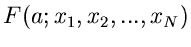 so zu
bestimmen, daß die Varianz
so zu
bestimmen, daß die Varianz 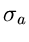 der Dichtefunktion
der Dichtefunktion 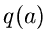 möglichst klein wird. Ein solches Verfahren ergibt den kleinsten
Meßfehler bei vorgegebener Stichprobe
möglichst klein wird. Ein solches Verfahren ergibt den kleinsten
Meßfehler bei vorgegebener Stichprobe
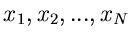 .
Die Antwort der Statistik auf diese Aufgabe ist das sogenannte Maximum-
Likelihood Verfahren:
.
Die Antwort der Statistik auf diese Aufgabe ist das sogenannte Maximum-
Likelihood Verfahren:
Satz: Die beste Schätzfunktion für die Bestimmung des Parameters 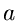 ist die Ableitung des Logarithmus der Dichtefunktion nach dem Parameter
ist die Ableitung des Logarithmus der Dichtefunktion nach dem Parameter 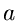 ,
,
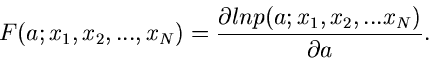 |
(4) |
Die aus der Bestimmungsgleichung
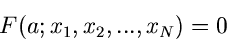 |
(5) |
berechnete zufällige Veränderliche 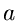 ist näherungsweise normalverteilt
mit der Varianz
ist näherungsweise normalverteilt
mit der Varianz
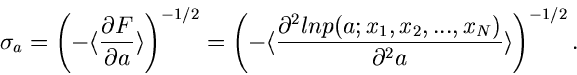 |
(6) |
Die Funktion
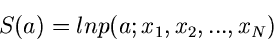 |
(7) |
nennt man die Likelihood Funktion.
Man kann also, und das ist für spätere Anwendungen von Bedeutung, das
Maximum- Likelihood Verfahren als Extremalaufgabe schreiben:
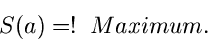 |
(8) |
Den aus einer einzigen Meßreihe
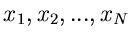 gewonnenen Wert
für
gewonnenen Wert
für 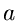 nennen wir im folgenden den Schätzwert
nennen wir im folgenden den Schätzwert 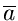 . Der Fehler
für
. Der Fehler
für 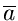 kann näherungsweise aus
kann näherungsweise aus
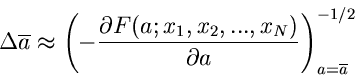 |
(9) |
berechnet werden.
Beispiel.
Eine einparametrige Wahrscheinlichkeitsverteilung ist die Poisson Verteilung
Es seien 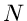 Messungen
Messungen 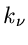 der zufälligen Veränderlichen
der zufälligen Veränderlichen 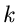 vorgelegt. Die Wahrscheinlichkeitsverteilung der unabhängigen Veränderlichen
vorgelegt. Die Wahrscheinlichkeitsverteilung der unabhängigen Veränderlichen
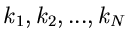 ist
ist
Die Funktion 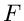 wird zu
wird zu
Aus 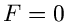 erhalten wir den besten Schätzwert für
erhalten wir den besten Schätzwert für 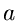 zu
zu
also den einfachen arithmetischen Mittelwert. Der Fehler der Messung berechnet
sich aus
zu
Mehrparametrige Verteilungen
Wir gehen weiter zu den Verteilungen mit mehreren Parametern:
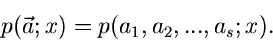 |
(10) |
In diesem Fall sind 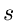 Funktionen zu suchen,
Funktionen zu suchen,
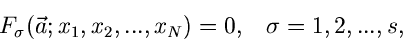 |
(11) |
und zwar so, daß die Norm der Kovarianzmatrix der Dichtefunktion
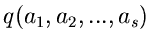 möglichst klein wird. Auch für diesen Fall
läßt sich zeigen, daß die Funktionen
möglichst klein wird. Auch für diesen Fall
läßt sich zeigen, daß die Funktionen
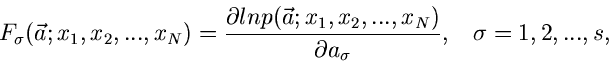 |
(12) |
die besten Schätzwerte für den Parametervektor 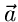 ergeben. Wie
bei den einparametrigen Verteilungen nennen wir
ergeben. Wie
bei den einparametrigen Verteilungen nennen wir
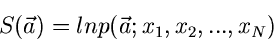 |
(13) |
die Likelohood Funktion. Im Gegensatz zu (2) handelt es sich
bei der Formel (11) allerdings um eine System mit 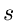 Gleichungen
und
Gleichungen
und 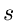 Unbekannten. Wir bilden die Ableitungen
Unbekannten. Wir bilden die Ableitungen
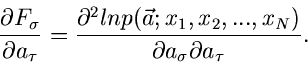 |
(14) |
In Verallgemeinerung zu (9) läßt sich zeigen, daß die Fehlermatrix
für die Schätzwerte
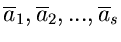 durch
durch
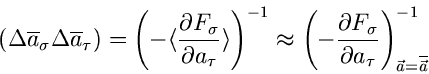 |
(15) |
gegeben ist. Man beachte, daß es sich hierbei um eine Matrizengleichung
handelt, insbesondere auf der rechten Seite der Gleichung um eine
Matrizeninversion. Als Fehler des Schätzwertes
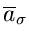 eines einzelnen Parameters gibt man im allgemeinen die Wurzel aus dem
Diagonalelement
eines einzelnen Parameters gibt man im allgemeinen die Wurzel aus dem
Diagonalelement
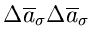 an.
an.
Beispiel.
Als Beispiel diskutieren wir die zweiparametrige Normalverteilung
Es seien 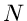 unabhängige Messungen
unabhängige Messungen
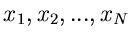 der zufälligen
Veränderlichen
der zufälligen
Veränderlichen 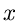 vorgegeben. Die gemeinsame Dichtefunktion ist
vorgegeben. Die gemeinsame Dichtefunktion ist
Das Gleichungssystem zur Bestimmung der Schätzwerte 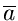 und
und
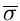 wird zu
wird zu
Die Lösung ist
Zur Bestimmung der Fehlermatrix berechnen wir
Wir bilden die Fehlermatrix an der Stelle
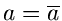 und
und
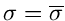 und erhalten
und erhalten
Die hierzu inverse Matrix ist
Daraus ergeben sich die Fehler der Schätzwerte zu
Mehrdimensionale Dichtefunktionen
Die Parameter Bestimmung bei mehrdimensionalen zufälligen Vektoren
ergibt keine neue Situation. Der zufällige Vektor
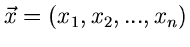 werde
werde 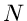 -mal unabhängig voneinander
gemessen, die Meßwerte seien
-mal unabhängig voneinander
gemessen, die Meßwerte seien
Die Kompenenten der Vektoren 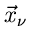 müssen jetzt natürlich
nicht unabhängig voneinander sein. Wir erhalten daher lediglich eine
Zerlegung der gesamten Dichtefunktion in der Form
müssen jetzt natürlich
nicht unabhängig voneinander sein. Wir erhalten daher lediglich eine
Zerlegung der gesamten Dichtefunktion in der Form
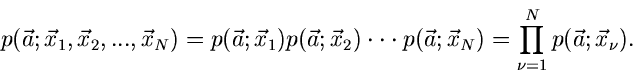 |
(16) |
Beispiel.
Als Beispiel betrachten wir die mehrdimensionale Normalverteilung
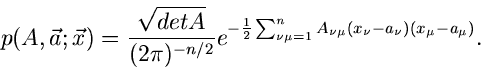 |
(17) |
Wir nehmen an, daß die Elemente der Matrix 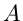 sowie der Erwartungswerte
sowie der Erwartungswerte
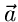 durch
durch 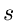 andere Parameter
andere Parameter
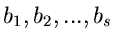 ausgedrückt werden können:
ausgedrückt werden können:
Dieses schließt offensichtlich den Fall ein, daß die Parameter 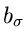 identisch mit den Parametern
identisch mit den Parametern 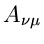 und
und 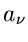 sind, und damit
sind, und damit
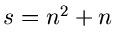 .
.
Seien 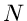 unabhängige Messungen des zufälligen Vektors
unabhängige Messungen des zufälligen Vektors 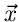 vorgelegt.
Die gemeinsame Dichtefunktion ist
vorgelegt.
Die gemeinsame Dichtefunktion ist
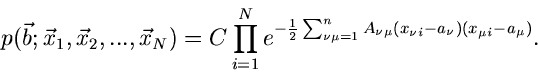 |
(20) |
mit
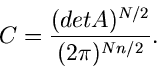 |
(21) |
Zur Vereinfachung schreiben wir im folgenden den Ausdruck im Exponenten
in Matrizen- und Vektorform (siehe Kap.3.2):
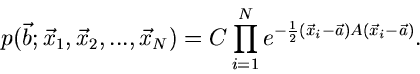 |
(22) |
Die Ableitungen vom Logarithmus dieser Dichtefunktion sind wie folgt:
Wegen
folgt
Bei dieser Umformung haben wir benutzt, daß
Zusammengefaßt erhalten wir
Die besten Parameterwerte nach dem Maximum Likelihood Verfahren findet man
dann aus dem Gleichungssytem
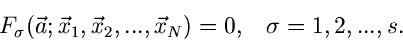 |
(27) |
Dieses ist ein hochgradig nichtlineares Gleichungssystem und kann im allgemeinen
nur mit numerischen Methoden gelöst werden. Hierzu werden wir wir am Ende
dieses Kapitels ein Verfahren angeben.
Die zweiten Ableitungen sind einfach und ergeben
Wir bilden die Erwartungswerte der zweiten Ableitungen. Mit Hilfe der
Formel (4.xx) erhalten wir
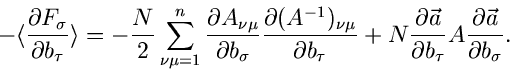 |
(29) |
Wegen der allgemeinen Matrizengleichung (siehe (3.xx))
und mit Einführung der Spur kann man diesen Ausdruck auch in der kompakten
Form
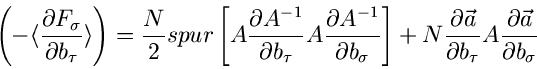 |
(30) |
schreiben. Die inverse Matrix hierzu ist dann die Fehlermatrix.
Wir haben dieses Beispiel in voller Länge durchgerechnet, da es uns in
den Anwendungen noch häufiger beschäftigen wird.
Die Näherung der kleinsten Quadrate
Das soeben durchgerechnete Maximum Likelihood Verfahren für die
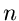 -dimensionale Normalverteilung kann stark vereinfacht werden, sobald die
Kovarianzmatrix bekannt ist, und somit nicht von den Parametern
-dimensionale Normalverteilung kann stark vereinfacht werden, sobald die
Kovarianzmatrix bekannt ist, und somit nicht von den Parametern 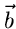 abhängt. In diesem Fall ist
abhängt. In diesem Fall ist
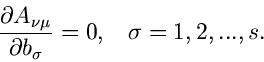 |
(31) |
Die Gleichungen (4.xx) und (4.xx) vereinfachen sich zu
Die Schätzfunktionen 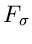 hätte man in diesem Fall auch aus
der Extremalbedingung
hätte man in diesem Fall auch aus
der Extremalbedingung
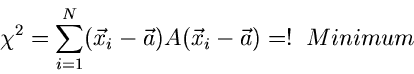 |
(34) |
schließen können. Falls
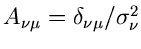 eine Diagonalmatrix ist, vereinfacht sich (4.xx) weiter zu
eine Diagonalmatrix ist, vereinfacht sich (4.xx) weiter zu
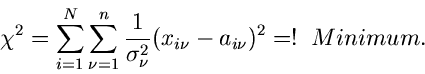 |
(35) |
In dieser letzten Form nennt man das Verfahren auch die Methode der
kleinsten Quadrate. Dieser Methode wollen wir uns im folgenden näher
zuwenden.
Die Methode der kleinsten Quadrate
Zur Einführung in die Methode der kleinsten Quadrate diskutieren wir zunächst
den Fall einer diskreten Veränderlichen 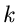 mit der
Wahrscheinlichkeitsverteilung
mit der
Wahrscheinlichkeitsverteilung 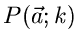 .
. 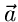 sei ein Vektor von
sei ein Vektor von
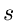 unbekannten Parametern,
unbekannten Parametern,
Es seien 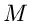 unabhängige Messungen der Veränderlichen
unabhängige Messungen der Veränderlichen 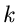 vorgelegt,
und zwar
vorgelegt,
und zwar
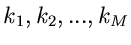 . Für hinreichend große
. Für hinreichend große 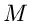 sind
natürlich nicht alle Messungen
sind
natürlich nicht alle Messungen 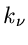 voneinander verschieden. Wir
nehmen an, daß ein bestimmter Wert
voneinander verschieden. Wir
nehmen an, daß ein bestimmter Wert 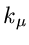 mit einer Häufigkeit
mit einer Häufigkeit
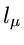 in der Meßreihe auftritt und setzen die Anzahl der verschiedenen
gemessenen Werte der Veränderlichen
in der Meßreihe auftritt und setzen die Anzahl der verschiedenen
gemessenen Werte der Veränderlichen 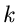 gleich
gleich 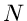 . Dann ist
. Dann ist
Die relative Häufigkeit
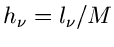 sollte dann, wie wir aus
Kap.2.4 her wissen, für große
sollte dann, wie wir aus
Kap.2.4 her wissen, für große 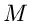 gegen die Wahrscheinlichkeit
gegen die Wahrscheinlichkeit
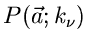 konvergieren:
konvergieren:
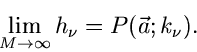 |
(36) |
Daraus ergibt sich offensichtlich die folgende Bedingung für die Bestimmung
der Parameter 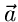 :
:
Satz: Bei der Methode der kleinsten Quadrate erhält man die besten
Parameterwerte aus der Extremalbedingung
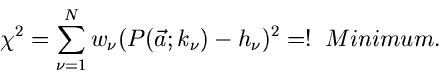 |
(37) |
Das Gewicht 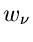 ist hierbei durch das inverse Quadrat des Fehlers der
relativen Häufigkeit gegeben:
ist hierbei durch das inverse Quadrat des Fehlers der
relativen Häufigkeit gegeben:
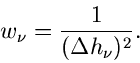 |
(38) |
Für
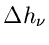 kann man entweder die Wurzel aus
kann man entweder die Wurzel aus 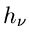 oder
die Wurzel aus
oder
die Wurzel aus
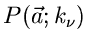 wählen, d.h.
wählen, d.h.
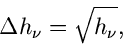 |
(39) |
oder
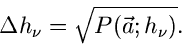 |
(40) |
Im Grenzfall 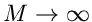 ergeben beide Fehler dasselbe Ergebnis.
Im letzteren Fall (40) tritt natürlich das Problem auf, daß man die
Parameterwerte
ergeben beide Fehler dasselbe Ergebnis.
Im letzteren Fall (40) tritt natürlich das Problem auf, daß man die
Parameterwerte 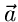 bereits kennen muß, um
bereits kennen muß, um
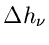 zu
berechnen. Man behilft sich hierbei, indem man möglichst gute, bereits
bekannte Werte für die Parameter in die Formel einsetzt. Im übrigen
gibt es seit Einführung der Methode der kleinsten Quadrate einen ewigen
Streit der Statistiker, welche der beiden Gewichtsfaktoren (39) oder
(40) die bessere Parameterbestimmung ergibt. Einer Diskussion der
Argumente wollen wir uns in diesem Buch nicht zuwenden.
zu
berechnen. Man behilft sich hierbei, indem man möglichst gute, bereits
bekannte Werte für die Parameter in die Formel einsetzt. Im übrigen
gibt es seit Einführung der Methode der kleinsten Quadrate einen ewigen
Streit der Statistiker, welche der beiden Gewichtsfaktoren (39) oder
(40) die bessere Parameterbestimmung ergibt. Einer Diskussion der
Argumente wollen wir uns in diesem Buch nicht zuwenden.
Das Minimum für die 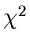 - Funktion wird an der Nullstelle der
Ableitung angenommen,
- Funktion wird an der Nullstelle der
Ableitung angenommen,
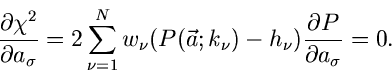 |
(41) |
Diese Bedingung ergibt die folgende Schätzfunktion für die Bestimmung der
Parameter 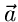 :
:
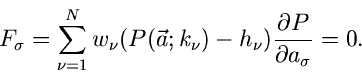 |
(42) |
Die Fehler für die Schätzwerte
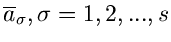 ergeben sich wiederum, wie wir es schon vom Maximum Likelihood Verfahren her
kennen, aus den partiellen Ableitungen der Schätzfunktion
ergeben sich wiederum, wie wir es schon vom Maximum Likelihood Verfahren her
kennen, aus den partiellen Ableitungen der Schätzfunktion 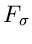 zu
zu
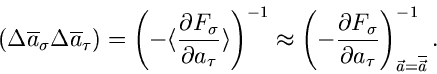 |
(43) |
Das Verfahren der kleinsten Quadrate kann ohne Schwierigkeit auf
kontinuierliche Veränderliche 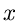 mit der Dichtefunktion
mit der Dichtefunktion 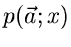 übertragen werden. Hierzu führen wir
eine Diskretisierung der Veränderlichen
übertragen werden. Hierzu führen wir
eine Diskretisierung der Veränderlichen 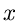 ein, d.h. wir bilden ein
Histogramm und identifizieren
ein, d.h. wir bilden ein
Histogramm und identifizieren
![\begin{displaymath}
k_{\nu} \equiv \{ x; x \in [x_{\nu},x_{\nu +1}] \} .
\end{displaymath}](img156.gif) |
(44) |
Die Wahrscheinlichkeitsverteilung ist dann
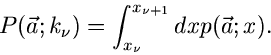 |
(45) |
In der allgemeinsten Form der Methode der kleinsten Quadrate sind 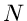 unabhängige Messungen
unabhängige Messungen 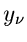 bei den Koordinaten
bei den Koordinaten 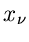 vorgegeben.
Die Fehler der Messungen seien mit
vorgegeben.
Die Fehler der Messungen seien mit 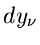 bezeichnet. Die Meßwerte
bezeichnet. Die Meßwerte
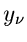 sollen durch eine Funktion
sollen durch eine Funktion
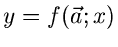 mit unbekannten
Parametern
mit unbekannten
Parametern
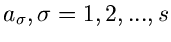 beschrieben werden. Hierbei
braucht es sich nicht um zufällige Veränderliche zu handeln. Die
beschrieben werden. Hierbei
braucht es sich nicht um zufällige Veränderliche zu handeln. Die
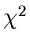 - Funktion wird definiert durch
- Funktion wird definiert durch
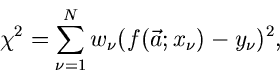 |
(46) |
mit
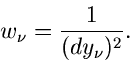 |
(47) |
Die besten Schätzwerte für die Parameter 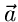 erhält man für das
Minimum der
erhält man für das
Minimum der 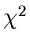 - Funktion,
- Funktion,
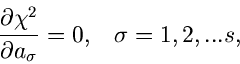 |
(48) |
d.h. mit Hilfe der Schätzfunktionen
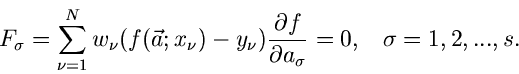 |
(49) |
Die Fehler dieser Parameterbestimmung berechnet man wie bisher mit Hilfe der
Matrizengleichung
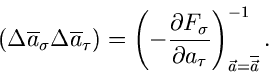 |
(50) |
Beispiel.
Im folgenden diskutieren wir eine typische Anwendung der Methode der kleinsten
Quadrate. Es seien 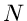 Messungen
Messungen 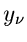 bei den Koordinaten
bei den Koordinaten 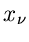 vorgegeben. Es werde angenommen, daß die Meßwerte
vorgegeben. Es werde angenommen, daß die Meßwerte 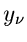 linear mit
den Koordinaten
linear mit
den Koordinaten 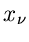 zusammenhängen, d.h.
zusammenhängen, d.h.
Die 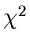 - Funktion lautet
- Funktion lautet
und die besten Schätzwerte für 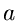 und
und 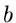 erhält man aus den Gleichungen
erhält man aus den Gleichungen
oder, nach Auflösen der Summen,
Dieses Gleichungssystem läßt sich leicht nach 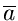 und
und
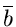 auflösen.
auflösen.
In Verallgemeinerung werde angenommen, daß die Meßwerte 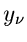 nicht
linear mit den Koordinaten
nicht
linear mit den Koordinaten 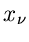 zusammenhängen, sondern daß diese
Abhängigkeit durch ein Polynom
zusammenhängen, sondern daß diese
Abhängigkeit durch ein Polynom 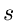 -ten Grades beschrieben werden kann,
-ten Grades beschrieben werden kann,
Wir erhalten dann
und
Dieses ergibt ein lineares Gleichungssystem mit 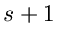 zu bestimmenden
Schätzwerten
zu bestimmenden
Schätzwerten
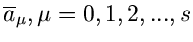 :
:
Die Poisson Methode
Eine etwas andere Methode wird häufig bei der Bestimmung von Parametern aus
Messungen von Zählraten angewandt. Angenommen, wir messen Zählraten
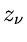 bei Koordinaten
bei Koordinaten 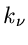 , und erwarten aufgrund theoretischer
Überlegungen Zählraten
, und erwarten aufgrund theoretischer
Überlegungen Zählraten
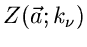 . Dann ist die
Wahrscheinlichkeit für eine Messung der Zählrate
. Dann ist die
Wahrscheinlichkeit für eine Messung der Zählrate 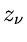 durch
durch
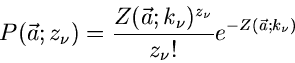 |
(51) |
gegeben. Bei  unabhängigen Messungen
unabhängigen Messungen
 bei den
Koordinaten
bei den
Koordinaten
 kann man die Gesamtwahrscheinlichkeit
als Produkt schreiben,
kann man die Gesamtwahrscheinlichkeit
als Produkt schreiben,
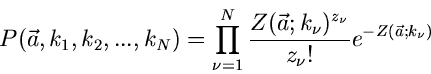 |
(52) |
und die besten Schätzfunktionen nach der Maximum Likelihood Methode sind
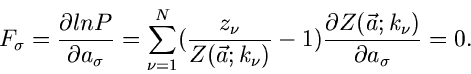 |
(53) |
Auf dieses Verfahren werden wir in späteren Anwendungen noch zurückkommen.
Ein Rechnerprogramm zur Bestimmung von Parametern
Alle drei Methoden, die Maximum Likelihood Methode, die Methode der kleinsten
Quadrate und die Poisson Methode können als Extremalaufgabe geschrieben
werden:
1. Maximum Likelihood Methode:
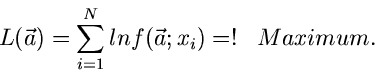 |
(54) |
2. Methode der kleinsten Quadrate:
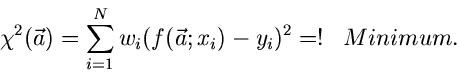 |
(55) |
3. Poisson- Methode:
![\begin{displaymath}
P(\vec{a}) = \sum_{i=1}^{N} [ y_{i} ln f(\vec{a}; x_{i}) - f(\vec{a}; x_{i})]
=! \; \; \; Maximum.
\end{displaymath}](img195.gif) |
(56) |
Man beachte allerdings die verschiedene Bedeutung der Funktion
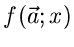 in diesen drei Ausdrücken. Die Bestimmungsgleichungen
für die Parameter
in diesen drei Ausdrücken. Die Bestimmungsgleichungen
für die Parameter
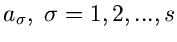 sowie die Ableitungen
für die Berechnung der Fehler sind:
sowie die Ableitungen
für die Berechnung der Fehler sind:
1. Maximum Likelihood Methode:
2. Methode der kleinsten Quadrate:
3. Poisson- Methode:
Zur Lösung dieser Gleichungen verwenden wir das einfache Newton
Verfahren. Dieses beruht auf der folgenden Iteration, die wir zunächst
für den Fall eines einzelnen Parameters erläutern.
Beginnend mit einem Startwert 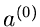 erhält man einen besseren Wert
für die Nullstelle der Funktion
erhält man einen besseren Wert
für die Nullstelle der Funktion 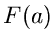 gemäß
gemäß
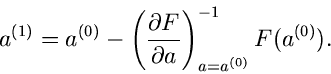 |
(63) |
Die Iteration besteht aus der weiteren Anwendung dieser Rekursion,
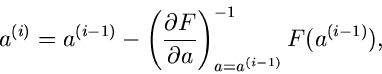 |
(64) |
bis entweder die Differenz
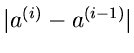 oder der Betrag von
oder der Betrag von
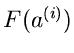 einen bestimmten vorgegebenen Wert unterschreitet. Offensichtlich
kann die Bedingung
einen bestimmten vorgegebenen Wert unterschreitet. Offensichtlich
kann die Bedingung
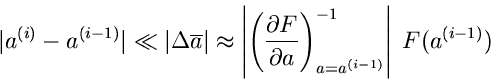 |
(65) |
zum Abbruch der Iteration herangezogen werden. Diese Iteration kann leicht
auf Gleichungssysteme übertragen werden:
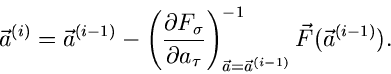 |
(66) |
Die Fehlermatrix ist am Ende der Iteration direkt durch
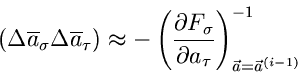 |
(67) |
gegeben, muß also nicht extra berechnet werden.
Ein Demonstrationsprogramm ist in dem
folgenden
Applet gegeben.
Mit Hilfe eines 1. Generators erzeugen wir Daten mit einer
bestimmten Verteilungsfunktion. Diese erste Verteilung kann noch mit einer 2. Verteilung
gefaltet werden, sodaß man insgesamt eine grosse Menge verschiedener Verteilungsfunktionen
erzeugen kann. Diese Gesamtverteilung kann dann mit dem Modell einer Normalverteilung,
einer Exponentialverteilung oder einer Poissonverteilung gefitted werden.
Als Beispiel zeigen wir in Abbildung 1 den Fit einer normalverteilten Simulation (linkes Fesnter)
mit einer Normalverteilung (rechtes Fenster). Die gefitten Parameter (a1 = Mittelwert, a2 = Varianz)
sind im Monitor- Fenster angezeigt.
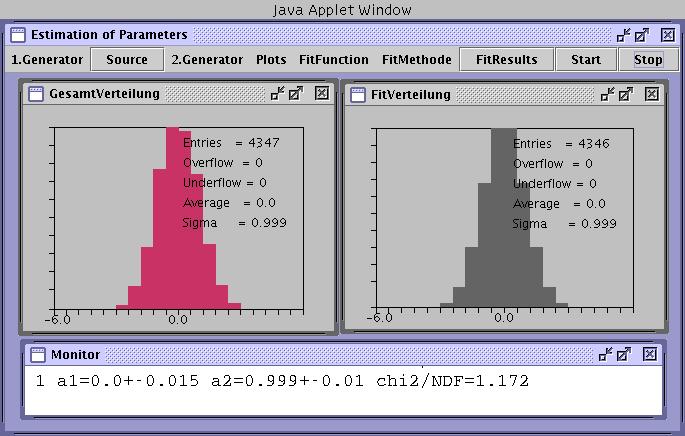
Abbildung 1:
Maximum Likelihood Fit einer normalverteilten Größe mit einer Normalverteilung.
In Abbildung 2 haben wir eine Bernoulli- Verteilung mit einer
Exponentialverteilung gefaltet. Daher wird der Ausläufer zu hohen Werten der Veränderlichen nochmals
stark erhöht. Diese Verteilung wurde ebenfalls mit einer Normalverteilung gefitted. Die Ergebnisse
im Monitorfenster zeigen ebenfalls gute Ergebnisse, die simulierte Verteilung und die gefittete Verteilung sind jedoch
total verschieden. Verteilung und Modell stimmen in diesem Fall nicht überein. Wie müssen
daher noch ein Kriterium diskutieren, um die Übereinstimmung von experimentellen Daten und Modell
zu prüfen.
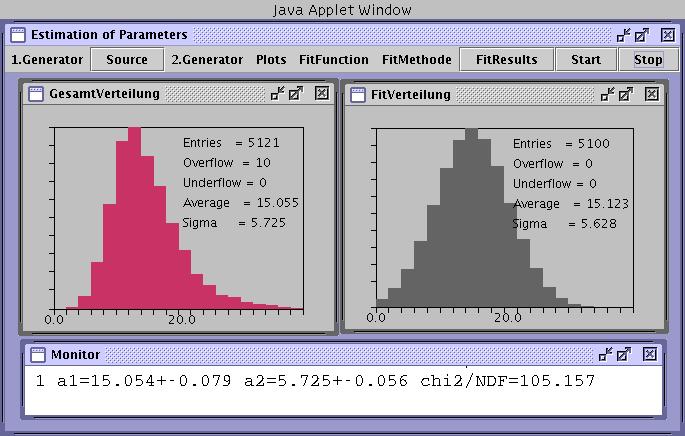
Abbildung 2:
Maximum Likelihood Fit einer verzerrten Bernoulliverteilung mit einem normalverteilten Modell.
Testen von Hypothesen
In vorigen Abschnitt haben wir diskutiert, wie die Parameter 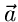 einer Wahrscheinlichkeitsverteilung
einer Wahrscheinlichkeitsverteilung
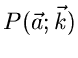 bzw einer
Dichtefunktion
bzw einer
Dichtefunktion
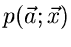 aus
aus 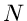 Messungen der Veränderlichen
Messungen der Veränderlichen
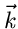 bzw
bzw 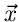 bestimmt werden können. Hierbei haben wir
stillschweigend angenommen, daß die gemessenen Veränderlichen wirklich
aus der Wahrscheinlichkeitsverteilung
bestimmt werden können. Hierbei haben wir
stillschweigend angenommen, daß die gemessenen Veränderlichen wirklich
aus der Wahrscheinlichkeitsverteilung
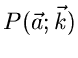 bzw aus der
Dichtefunktion
bzw aus der
Dichtefunktion
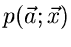 stammen. Diese Annahme ist in der
Praxis jedoch nur selten gerechtfertigt. Die Veränderlichen
stammen. Diese Annahme ist in der
Praxis jedoch nur selten gerechtfertigt. Die Veränderlichen 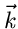 bzw
bzw 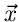 sind das Ergebnis eines Versuches mit unbekanntem
Bedingungskomplex, die Wahrscheinlichkeitsverteilung bzw Dichtefunktion
ist daher eine hypothetische Annahme. Es bleibt also noch zu prüfen,
wie gut diese Hypothese mit den Messungen des Experiment übereinstimmt.
Es ergibt sich daher folgende Situation. Wir haben
sind das Ergebnis eines Versuches mit unbekanntem
Bedingungskomplex, die Wahrscheinlichkeitsverteilung bzw Dichtefunktion
ist daher eine hypothetische Annahme. Es bleibt also noch zu prüfen,
wie gut diese Hypothese mit den Messungen des Experiment übereinstimmt.
Es ergibt sich daher folgende Situation. Wir haben 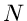 Messungen der
Veränderlichen
Messungen der
Veränderlichen 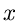 (wir beschränken uns zunächst auf eindimensionale
Veränderliche). Aus Überlegungen irgendwelcher Art stellen wir die
Hypothese auf, daß die Dichtefunktion
(wir beschränken uns zunächst auf eindimensionale
Veränderliche). Aus Überlegungen irgendwelcher Art stellen wir die
Hypothese auf, daß die Dichtefunktion 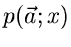 den Bedingungskomplex
unseres Versuches beschreibt und bestimmen mit einem der im vorigen
Abschnitt diskutierten Verfahren die optimalen Werte der Parameter
den Bedingungskomplex
unseres Versuches beschreibt und bestimmen mit einem der im vorigen
Abschnitt diskutierten Verfahren die optimalen Werte der Parameter 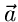 .
Hierbei erhalten wir immer irdendwelche Parameterwerte, unabhängig davon,
ob die Dichtefunktion
.
Hierbei erhalten wir immer irdendwelche Parameterwerte, unabhängig davon,
ob die Dichtefunktion 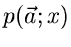 wirklich den Bedingungskomplex des
Experiments beschreibt oder auch nicht. Dieses erkennt man im allgemeinen
auch nicht an den Fehlern der Parameter. Die Fehler können beliebig
klein sein, obwohl die Dichtefunktion völlig falsch war. Abschließend
müssen wir daher testen, ob die Hypothese
wirklich den Bedingungskomplex des
Experiments beschreibt oder auch nicht. Dieses erkennt man im allgemeinen
auch nicht an den Fehlern der Parameter. Die Fehler können beliebig
klein sein, obwohl die Dichtefunktion völlig falsch war. Abschließend
müssen wir daher testen, ob die Hypothese 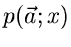 für die
vorgegebenen Messungen
für die
vorgegebenen Messungen
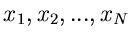 akzeptiert werden kann.
akzeptiert werden kann.
Hierzu gibt es sehr viele verschiedene Testverfahren, die zumindest
zum Teil auf spezielle Probleme zugeschnitten sind. Wir hatten
bereits die speziellen Verfahren des Korrelationstests und des
Phasentests im Zusammenhang mit den Pseudozufallszahlen diskutiert.
Allen Testverfahren gemeinsam ist, daß, ähnlich wie bei der
Parameterbestimmung, eine skalare Testfunktion definiert wird,
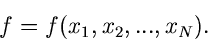 |
(68) |
Die Größe 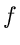 ist wiederum eine zufällige Veränderliche mit einer
Dichtefunktion
ist wiederum eine zufällige Veränderliche mit einer
Dichtefunktion 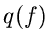 . Diese Dichtefunktion kann durch die Dichtefunktion
. Diese Dichtefunktion kann durch die Dichtefunktion
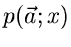 ausgedrückt werden gemäß:
ausgedrückt werden gemäß:
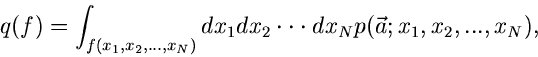 |
(69) |
mit
Ähnlich wie bei der Parameterbestimmung kann man auch hier nach einer
''besten'' Testfunktion fragen. Dieser Frage werden wir uns in diesem
Buch jedoch nicht widmen, sondern sofort zu dem am häufigsten angewendeten
Testverfahren übergehen, nämlich zum 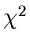 - Test.
- Test.
Die 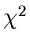 - Verteilung
- Verteilung
Wir sortieren die 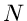 Messungen
Messungen
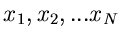 in ein Histogramm mit
in ein Histogramm mit
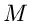 Intervallen zwischen den Stützstellen
Intervallen zwischen den Stützstellen
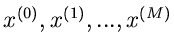 .
Falls die hypothetisch angenommene Dichtefunktion
.
Falls die hypothetisch angenommene Dichtefunktion
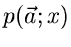 auf der gesamten reellen Achse definiert ist, setzen wir
die unterste und oberste Intervallgrenze zu
auf der gesamten reellen Achse definiert ist, setzen wir
die unterste und oberste Intervallgrenze zu
Die Anzahl der Meßwerte in jedem dieser Intervalle sei
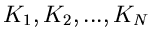 . Die Wahrscheinlichkeitsverteilung ist durch
. Die Wahrscheinlichkeitsverteilung ist durch
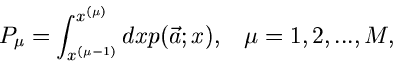 |
(70) |
für kontinuierliche Veränderliche bzw durch
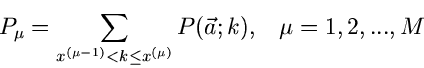 |
(71) |
für diskrete Veränderliche gegeben. Die hier geschilderte Situation
entspricht nun genau der Definition der Multinominalverteilung.
Daher ist die Wahrscheinlichkeit, genau 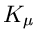
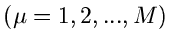 Messungen in den Intervallen
Messungen in den Intervallen
![$(x^{(\mu-1)},x^{(\mu)}]$](img230.gif) zu erhalten, durch die Multinominalverteilung
zu erhalten, durch die Multinominalverteilung
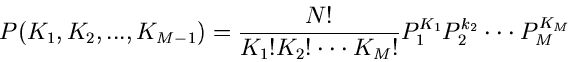 |
(72) |
mit
gegeben. Man beachte, daß diese Verteilung nur 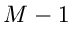 zufällige
Veränderliche hat. Genau wie im Fall der einfachen Bernoulli- Verteilung
(mit
zufällige
Veränderliche hat. Genau wie im Fall der einfachen Bernoulli- Verteilung
(mit 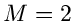 ) kann die Multinominalverteilung für große
) kann die Multinominalverteilung für große 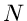 durch eine
durch eine
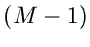 - dimensionale Normalverteilung approximiert werden.
Aus der erzeugenden Funktion der Multinominalverteilung,
- dimensionale Normalverteilung approximiert werden.
Aus der erzeugenden Funktion der Multinominalverteilung,
![\begin{displaymath}
M_{K_{1},K_{2},...,K_{M-1}}(v_{1},v_{2},...,v_{M-1}) =
[ 1+ \sum_{\mu=1}^{M-1} (e^{v_{\mu}} -1) P_{\mu} ]^{N},
\end{displaymath}](img239.gif) |
(75) |
erhalten wir
und
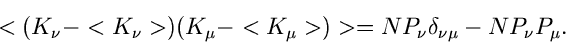 |
(78) |
Zur Vereinfachung der Schreibweise setzen wir
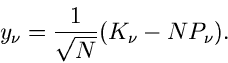 |
(79) |
Diese Größe besitzt die Mittelwerte und Kovarianzmatrix
Die Kovarianzmatrix 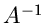 läßt sich leicht analytisch invertieren, und
zwar
läßt sich leicht analytisch invertieren, und
zwar
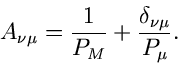 |
(82) |
Daraus erhalten wir die Verteilungsfunktion der Abweichungen 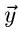 zu
zu
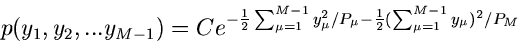 |
(83) |
mit
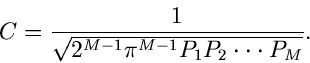 |
(84) |
In der obigen Ableitung haben wir benutzt, daß
ist. Als neue Variable führen wir die Größe
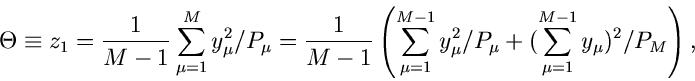 |
(85) |
sowie die Hilfstransformationen
ein. Die Transformation der Verteilungsfunktion von der zufälligen
Veränderlichen 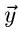 auf die zufällige Veränderliche
auf die zufällige Veränderliche 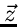 und nachfolgende Integration (Reduktion) über die Hilfsgrößen
und nachfolgende Integration (Reduktion) über die Hilfsgrößen
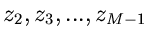 führt nach einiger Rechnung auf die Dichtefunktion
für die Veränderliche
führt nach einiger Rechnung auf die Dichtefunktion
für die Veränderliche
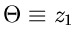 :
:
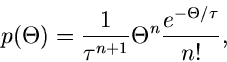 |
(86) |
mit
Diese spezielle Gammafunktion nennt man auch die 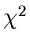 - Verteilung.
Sie hängt offensichtlich nur noch von der Anzahl
- Verteilung.
Sie hängt offensichtlich nur noch von der Anzahl 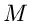 der Histogramm-
Intervalle ab, jedoch nicht von der ursprünglichen Dichtefunktion
der Histogramm-
Intervalle ab, jedoch nicht von der ursprünglichen Dichtefunktion
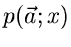 bzw den Wahrscheinlichkeiten
bzw den Wahrscheinlichkeiten
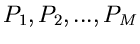 .
Die erzeugende Funktion der
.
Die erzeugende Funktion der 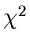 - Verteilung ergibt sich zu
- Verteilung ergibt sich zu
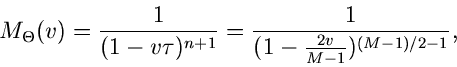 |
(87) |
und die logarithmisch erzeugende Funktion zu
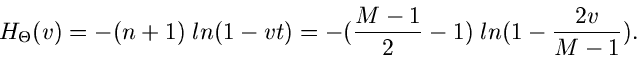 |
(88) |
Aus der Reihenentwicklung
erhalten wir die ersten beiden Momente der 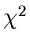 - Verteilung:
- Verteilung:
Dieses ist exakt das Ergebnis, das wir bereits im ersten Teil dieses Tutorials
ohne Beweis benutzt hatten. Dort hatten wir eine
weitere Größe eingeführt, nämlich
Die Dichtefunktion dieser Veränderlichen besitzt zwar die von 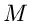 unabhängigen ersten beiden Momente
unabhängigen ersten beiden Momente
alle höheren Momente hängen aber weiterhin von 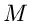 ab. Da die Dichtefunktion
der Veränderlichen
ab. Da die Dichtefunktion
der Veränderlichen 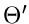 wesentlich komplizierter als die der Größe
wesentlich komplizierter als die der Größe
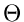 ist, benutzen wir im folgenden den
ist, benutzen wir im folgenden den 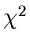 - Test mit der
Veränderlichen
- Test mit der
Veränderlichen 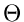 . Die Größe
. Die Größe 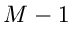 nennt man die Anzahl
der Freiheitsgrade (NDF = ''Number Degrees of Freedom'').
nennt man die Anzahl
der Freiheitsgrade (NDF = ''Number Degrees of Freedom'').
Der 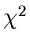 - Test
- Test
Zusammenfassend geben wir noch einmal die Schritte an, die zum 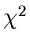 -
Test führen:
-
Test führen:
1. Aus einem Versuch erhalten wir 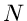 unabhängige Messungen der
zufälligen Veränderlichen
unabhängige Messungen der
zufälligen Veränderlichen 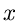 , und zwar
, und zwar
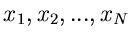 .
.
2. Wir sortieren die Messungen in ein Histogramm mit 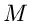 Intervallen
zwischen den Stützstellen
Intervallen
zwischen den Stützstellen
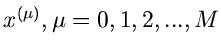 . Die Häufigkeiten
in den Intervallen seien
. Die Häufigkeiten
in den Intervallen seien
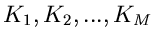 .
.
3. Aus der Hypothese, daß die Dichtefunktion 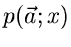 den
Bedingungskomplex des Versuches vollständig beschreibt, erhalten wir die
hypothetischen Wahrscheinlichkeiten
den
Bedingungskomplex des Versuches vollständig beschreibt, erhalten wir die
hypothetischen Wahrscheinlichkeiten
4. Wir bilden das sogenannte 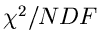 ,
,
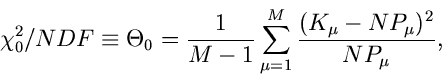 |
(91) |
und berechnen die Wahrscheinlichkeit dafür, daß die Veränderliche
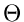 einen Wert größer als den gemessenen Wert
einen Wert größer als den gemessenen Wert 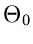 annimmt:
annimmt:
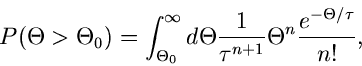 |
(92) |
mit
Diese Wahrscheinlichkeit, ausgedrückt in 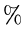 , nennt man gemeinhin auch
den
, nennt man gemeinhin auch
den 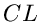 (Confidence Level).
(Confidence Level).
5. Das Ergebnis lautet: Mit einem Confidence Level von 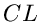
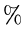 erfüllt
die Dichtefunktion
erfüllt
die Dichtefunktion 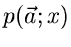 den Bedingungskomplex des Versuches mit
den Messungen
den Bedingungskomplex des Versuches mit
den Messungen
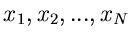 .
.
Der 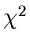 - Test ist erweiterungsfähig auf den allgemeinen Fall, daß
- Test ist erweiterungsfähig auf den allgemeinen Fall, daß
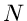 Messungen
Messungen
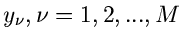 , mit den Meßfehlern
, mit den Meßfehlern 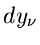 bei
den Koordinaten
bei
den Koordinaten 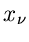 gegeben sind. Wir nehmen an, daß die Messungen
durch eine Funktion der Form
gegeben sind. Wir nehmen an, daß die Messungen
durch eine Funktion der Form 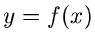 beschrieben werden können und bilden
das
beschrieben werden können und bilden
das 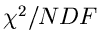 ,
,
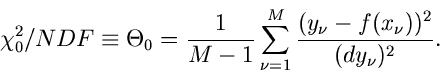 |
(93) |
Diese Veränderliche gehorcht allerdings nur dann der 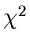 -
Verteilung, sofern die Meßfehler rein statistischer Natur sind.
-
Verteilung, sofern die Meßfehler rein statistischer Natur sind.
Harm Fesefeldt
2006-05-09
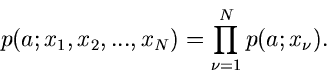
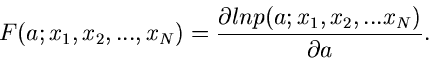
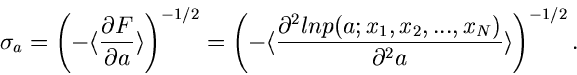
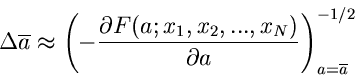
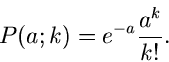
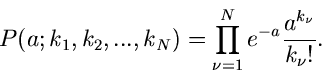
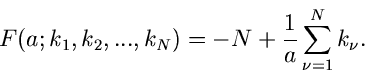
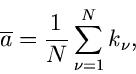
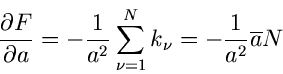
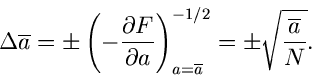
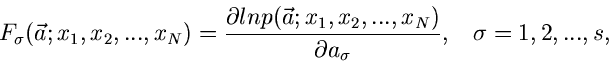
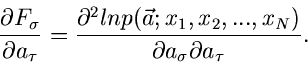
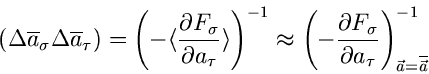
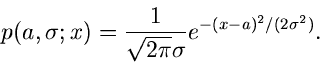
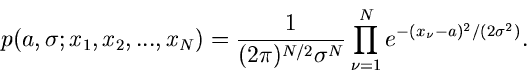
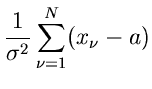
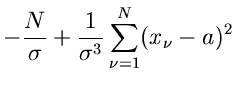
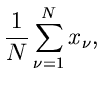
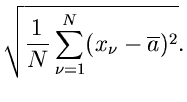
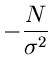
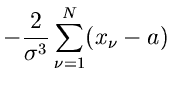
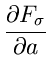
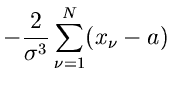
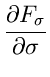
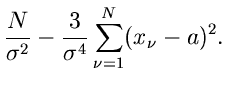
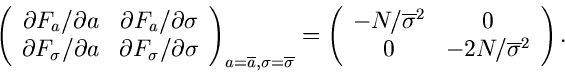
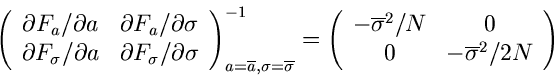
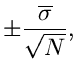
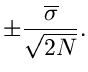
![]() werde
werde ![]() -mal unabhängig voneinander
gemessen, die Meßwerte seien
-mal unabhängig voneinander
gemessen, die Meßwerte seien
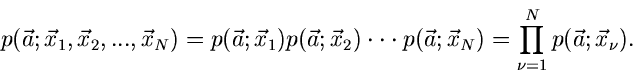
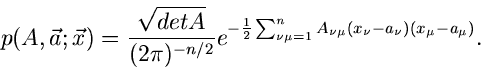
![]() unabhängige Messungen des zufälligen Vektors
unabhängige Messungen des zufälligen Vektors ![]() vorgelegt.
Die gemeinsame Dichtefunktion ist
vorgelegt.
Die gemeinsame Dichtefunktion ist
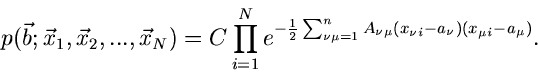
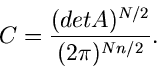
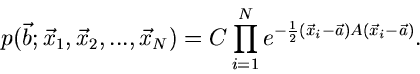
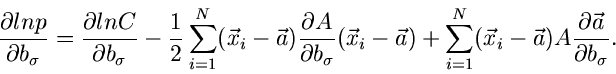
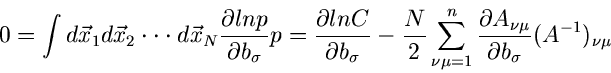
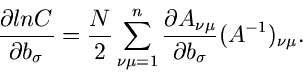
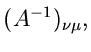
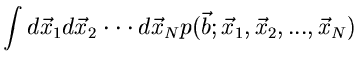
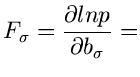
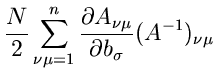
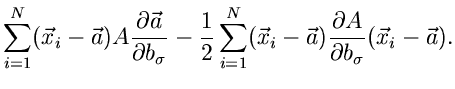
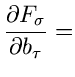
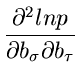
![$\displaystyle \frac{N}{2} \sum_{\nu\mu=1}^{n} \left[
\frac{\partial^{2} A_{\nu\...
...partial b_{\sigma}}
\frac{\partial(A^{-1})_{\nu\mu}}{\partial b_{\tau}} \right]$](img115.gif)
![$\displaystyle \sum_{i=1}^{N} \left[ -\frac{\partial \vec{a}}{\partial b_{\tau}}...
...}) A
\frac{\partial^{2} \vec{a}}{\partial b_{\sigma} \partial b_{\tau}} \right]$](img116.gif)
![$\displaystyle \sum_{i=1}^{N} \left[ (\vec{x}_{i}-\vec{a})
\frac{\partial A}{\pa...
...l^{2} A}{\partial b_{\sigma} \partial b_{\tau}}
(\vec{x}_{i}-\vec{a}) \right] .$](img117.gif)
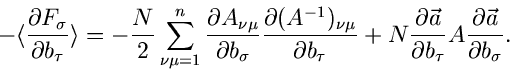
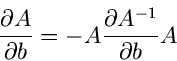
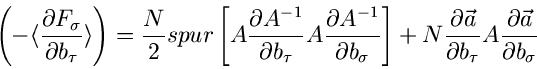
![]() -dimensionale Normalverteilung kann stark vereinfacht werden, sobald die
Kovarianzmatrix bekannt ist, und somit nicht von den Parametern
-dimensionale Normalverteilung kann stark vereinfacht werden, sobald die
Kovarianzmatrix bekannt ist, und somit nicht von den Parametern ![]() abhängt. In diesem Fall ist
abhängt. In diesem Fall ist
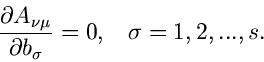
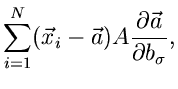
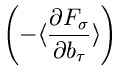
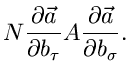
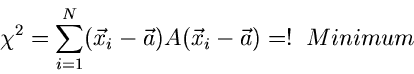
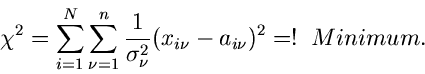
![]() mit der
Wahrscheinlichkeitsverteilung
mit der
Wahrscheinlichkeitsverteilung ![]() .
. ![]() sei ein Vektor von
sei ein Vektor von
![]() unbekannten Parametern,
unbekannten Parametern,
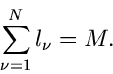
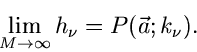
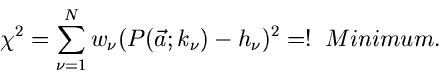
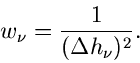
![]() - Funktion wird an der Nullstelle der
Ableitung angenommen,
- Funktion wird an der Nullstelle der
Ableitung angenommen,
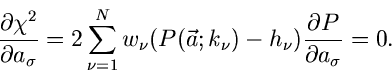
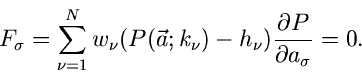
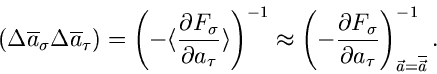
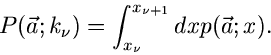
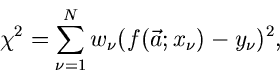
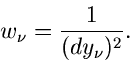
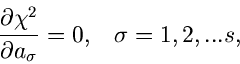
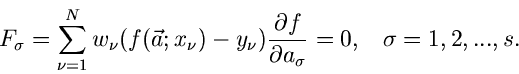
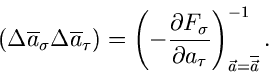
![]() Messungen
Messungen ![]() bei den Koordinaten
bei den Koordinaten ![]() vorgegeben. Es werde angenommen, daß die Meßwerte
vorgegeben. Es werde angenommen, daß die Meßwerte ![]() linear mit
den Koordinaten
linear mit
den Koordinaten ![]() zusammenhängen, d.h.
zusammenhängen, d.h.
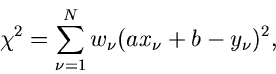
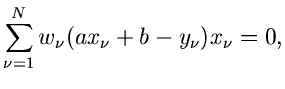
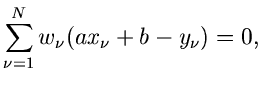
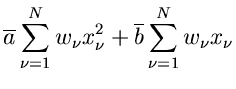
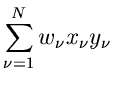
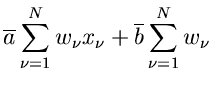
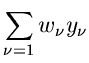
![]() nicht
linear mit den Koordinaten
nicht
linear mit den Koordinaten ![]() zusammenhängen, sondern daß diese
Abhängigkeit durch ein Polynom
zusammenhängen, sondern daß diese
Abhängigkeit durch ein Polynom ![]() -ten Grades beschrieben werden kann,
-ten Grades beschrieben werden kann,
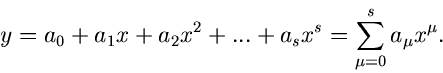
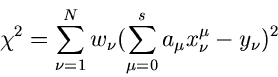
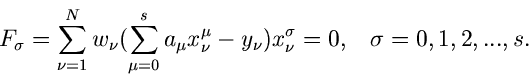
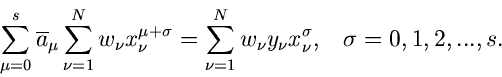
![]() bei Koordinaten
bei Koordinaten ![]() , und erwarten aufgrund theoretischer
Überlegungen Zählraten
, und erwarten aufgrund theoretischer
Überlegungen Zählraten
![]() . Dann ist die
Wahrscheinlichkeit für eine Messung der Zählrate
. Dann ist die
Wahrscheinlichkeit für eine Messung der Zählrate ![]() durch
durch
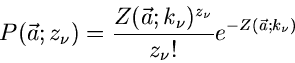
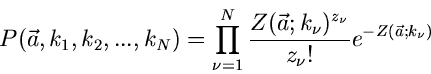
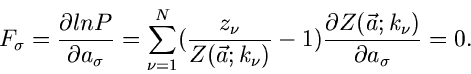
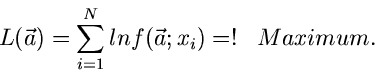
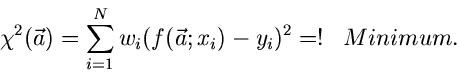
![\begin{displaymath}
P(\vec{a}) = \sum_{i=1}^{N} [ y_{i} ln f(\vec{a}; x_{i}) - f(\vec{a}; x_{i})]
=! \; \; \; Maximum.
\end{displaymath}](img195.gif)
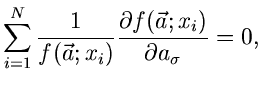
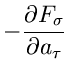
![$\displaystyle \sum_{i=1}^{N}
\frac{1}{f^{2}(\vec{a};x_{i})} \left[ \frac{\parti...
...};x_{i})
\frac{\partial^{2} f}{\partial a_{\sigma} \partial a_{\tau}} \right] .$](img200.gif)
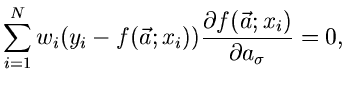
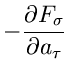
![$\displaystyle \sum_{i=1}^{N}
w_{i} \left[ \frac{\partial f}{\partial a_{\sigma}...
...;x_{i}))
\frac{\partial^{2} f}{\partial a_{\sigma} \partial a_{\tau}} \right] .$](img202.gif)
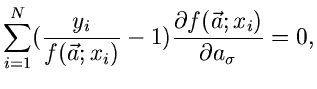
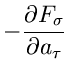
![$\displaystyle \sum_{i=1}^{N}
\left( \frac{y_{i}}{f^{2}(\vec{a};x_{i})} \left[
\...
...right] - \frac{\partial^{2} f}{\partial a_{\sigma} \partial a_{\tau}} \right) .$](img204.gif)
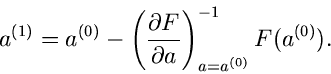
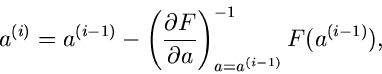
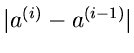 oder der Betrag von
oder der Betrag von
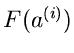 einen bestimmten vorgegebenen Wert unterschreitet. Offensichtlich
kann die Bedingung
einen bestimmten vorgegebenen Wert unterschreitet. Offensichtlich
kann die Bedingung
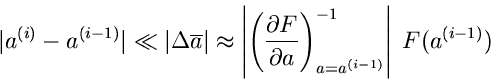
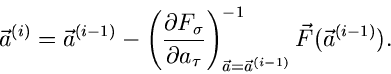
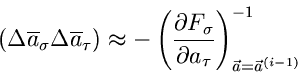


![]() einer Wahrscheinlichkeitsverteilung
einer Wahrscheinlichkeitsverteilung
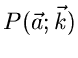 bzw einer
Dichtefunktion
bzw einer
Dichtefunktion
![]() aus
aus ![]() Messungen der Veränderlichen
Messungen der Veränderlichen
![]() bzw
bzw ![]() bestimmt werden können. Hierbei haben wir
stillschweigend angenommen, daß die gemessenen Veränderlichen wirklich
aus der Wahrscheinlichkeitsverteilung
bestimmt werden können. Hierbei haben wir
stillschweigend angenommen, daß die gemessenen Veränderlichen wirklich
aus der Wahrscheinlichkeitsverteilung
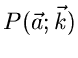 bzw aus der
Dichtefunktion
bzw aus der
Dichtefunktion
![]() stammen. Diese Annahme ist in der
Praxis jedoch nur selten gerechtfertigt. Die Veränderlichen
stammen. Diese Annahme ist in der
Praxis jedoch nur selten gerechtfertigt. Die Veränderlichen ![]() bzw
bzw ![]() sind das Ergebnis eines Versuches mit unbekanntem
Bedingungskomplex, die Wahrscheinlichkeitsverteilung bzw Dichtefunktion
ist daher eine hypothetische Annahme. Es bleibt also noch zu prüfen,
wie gut diese Hypothese mit den Messungen des Experiment übereinstimmt.
Es ergibt sich daher folgende Situation. Wir haben
sind das Ergebnis eines Versuches mit unbekanntem
Bedingungskomplex, die Wahrscheinlichkeitsverteilung bzw Dichtefunktion
ist daher eine hypothetische Annahme. Es bleibt also noch zu prüfen,
wie gut diese Hypothese mit den Messungen des Experiment übereinstimmt.
Es ergibt sich daher folgende Situation. Wir haben ![]() Messungen der
Veränderlichen
Messungen der
Veränderlichen ![]() (wir beschränken uns zunächst auf eindimensionale
Veränderliche). Aus Überlegungen irgendwelcher Art stellen wir die
Hypothese auf, daß die Dichtefunktion
(wir beschränken uns zunächst auf eindimensionale
Veränderliche). Aus Überlegungen irgendwelcher Art stellen wir die
Hypothese auf, daß die Dichtefunktion ![]() den Bedingungskomplex
unseres Versuches beschreibt und bestimmen mit einem der im vorigen
Abschnitt diskutierten Verfahren die optimalen Werte der Parameter
den Bedingungskomplex
unseres Versuches beschreibt und bestimmen mit einem der im vorigen
Abschnitt diskutierten Verfahren die optimalen Werte der Parameter ![]() .
Hierbei erhalten wir immer irdendwelche Parameterwerte, unabhängig davon,
ob die Dichtefunktion
.
Hierbei erhalten wir immer irdendwelche Parameterwerte, unabhängig davon,
ob die Dichtefunktion ![]() wirklich den Bedingungskomplex des
Experiments beschreibt oder auch nicht. Dieses erkennt man im allgemeinen
auch nicht an den Fehlern der Parameter. Die Fehler können beliebig
klein sein, obwohl die Dichtefunktion völlig falsch war. Abschließend
müssen wir daher testen, ob die Hypothese
wirklich den Bedingungskomplex des
Experiments beschreibt oder auch nicht. Dieses erkennt man im allgemeinen
auch nicht an den Fehlern der Parameter. Die Fehler können beliebig
klein sein, obwohl die Dichtefunktion völlig falsch war. Abschließend
müssen wir daher testen, ob die Hypothese ![]() für die
vorgegebenen Messungen
für die
vorgegebenen Messungen
![]() akzeptiert werden kann.
akzeptiert werden kann.
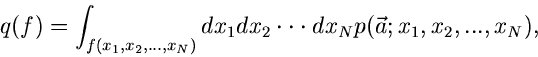
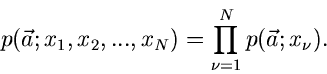
![]() - Verteilung
- Verteilung ![]() Messungen
Messungen
![]() in ein Histogramm mit
in ein Histogramm mit
![]() Intervallen zwischen den Stützstellen
Intervallen zwischen den Stützstellen
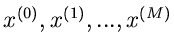 .
Falls die hypothetisch angenommene Dichtefunktion
.
Falls die hypothetisch angenommene Dichtefunktion
![]() auf der gesamten reellen Achse definiert ist, setzen wir
die unterste und oberste Intervallgrenze zu
auf der gesamten reellen Achse definiert ist, setzen wir
die unterste und oberste Intervallgrenze zu
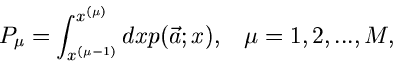
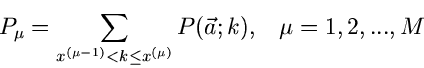
![$(x^{(\mu-1)},x^{(\mu)}]$](img230.gif) zu erhalten, durch die Multinominalverteilung
zu erhalten, durch die Multinominalverteilung
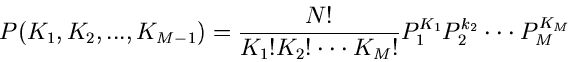
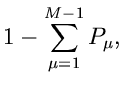
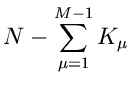
![\begin{displaymath}
M_{K_{1},K_{2},...,K_{M-1}}(v_{1},v_{2},...,v_{M-1}) =
[ 1+ \sum_{\mu=1}^{M-1} (e^{v_{\mu}} -1) P_{\mu} ]^{N},
\end{displaymath}](img239.gif)
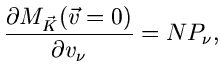
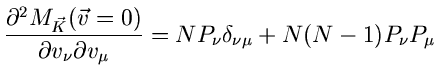
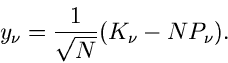
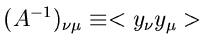
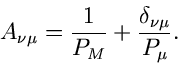
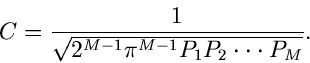
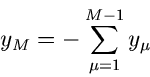
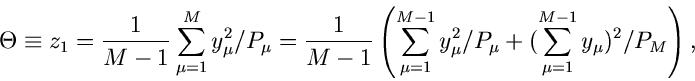
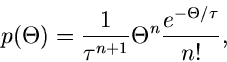
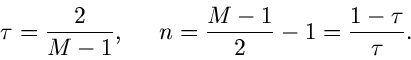
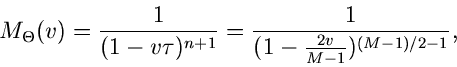
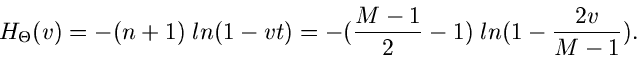
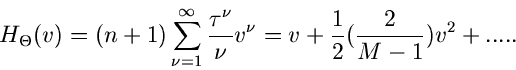
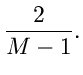
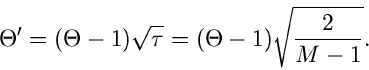
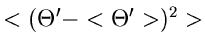
![]() - Test
- Test ![]() -
Test führen:
-
Test führen: ![]() unabhängige Messungen der
zufälligen Veränderlichen
unabhängige Messungen der
zufälligen Veränderlichen ![]() , und zwar
, und zwar
![]() .
. ![]() Intervallen
zwischen den Stützstellen
Intervallen
zwischen den Stützstellen
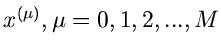 . Die Häufigkeiten
in den Intervallen seien
. Die Häufigkeiten
in den Intervallen seien
![]() .
. ![]() den
Bedingungskomplex des Versuches vollständig beschreibt, erhalten wir die
hypothetischen Wahrscheinlichkeiten
den
Bedingungskomplex des Versuches vollständig beschreibt, erhalten wir die
hypothetischen Wahrscheinlichkeiten
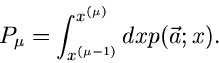
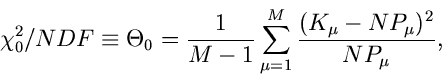
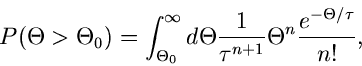
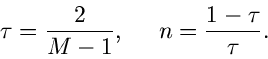
![]() - Test ist erweiterungsfähig auf den allgemeinen Fall, daß
- Test ist erweiterungsfähig auf den allgemeinen Fall, daß
![]() Messungen
Messungen
![]() , mit den Meßfehlern
, mit den Meßfehlern ![]() bei
den Koordinaten
bei
den Koordinaten ![]() gegeben sind. Wir nehmen an, daß die Messungen
durch eine Funktion der Form
gegeben sind. Wir nehmen an, daß die Messungen
durch eine Funktion der Form ![]() beschrieben werden können und bilden
das
beschrieben werden können und bilden
das ![]() ,
,