Inverse Transformation
Inverse Laplace- Transformation
Wir hatten im Zusammenhang mit unserem mathematischen Steilkurs die inverse
Laplace- Transformation bereits ausgiebig diskutiert. Angewendet auf den
hier vorliegenden Fall ergibt sich folgende Situation.
Wir nehmen an, daß aus Messungen eines Experimentes alle logarithmischen
Momente 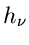 gemessen worden sind. Dann ist die logarithmisch
erzeugende Funktion:
gemessen worden sind. Dann ist die logarithmisch
erzeugende Funktion:
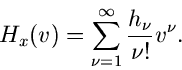 |
(1) |
Die logarithmischen Momente können wiederum aus irdendeinem anderen Satz von
Momenten berechnet werden. Oder aber, und dieses ist die zweite häufig
vorkommende Situation, wir haben die logarithmisch erzeugende Funktion
von einer Summe unabhängiger zufälliger Veränderlicher mit Hilfe einer
Faltung bestimmt. Den letzteren Fall hatten wir ausgiebig im vorherigen
Unterkapitel diskutiert. In beiden Fällen können wir davon ausgehen,
daß eine analytische Form der logarithmisch erzeugenden Funktion
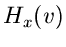 bekannt ist. Die Beziehung zwischen der logarithmisch erzeugenden
und der normalen erzeugenden Funktion (Laplace- Transformation) lautete:
bekannt ist. Die Beziehung zwischen der logarithmisch erzeugenden
und der normalen erzeugenden Funktion (Laplace- Transformation) lautete:
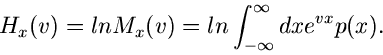 |
(2) |
Wendet man hierauf die inverse Laplace- Transformation an, so
erhält man:
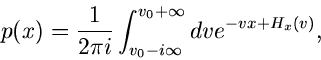 |
(3) |
wobei das Integral auf einer Geraden parallel zur imaginären Achse berechnet
werden muß und die reelle Zahl 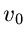 so gewählt werden muß, daß das
Integral existiert. Die Lösung dieses Integrals könnte auch mit Hilfe
des gesamten Formalismus der Residuen- Theorie vorgenommen werden.
Für die Form des Integral (3)
gibt es aber eine wesentlich einfachere Lösung, das sogenannte
Sattelpunkt- Verfahren.
so gewählt werden muß, daß das
Integral existiert. Die Lösung dieses Integrals könnte auch mit Hilfe
des gesamten Formalismus der Residuen- Theorie vorgenommen werden.
Für die Form des Integral (3)
gibt es aber eine wesentlich einfachere Lösung, das sogenannte
Sattelpunkt- Verfahren.
Das Sattelpunkt- Verfahren
Die Herleitung des Sattelpunkt- Verfahrens ist mit relativ viel Rechenarbeit
verbunden und wird daher im Rahmen dieses Lehrgangs nicht durchgeführt.
Für den interessierten Leser skizzieren wir nur kurz den Gang der Herleitung.
Wir machen den Ansatz
In dieser Entwicklung ist 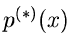 die erste Näherung des Sattelpunkt-
Verfahrens:
die erste Näherung des Sattelpunkt-
Verfahrens:
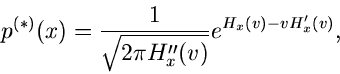 |
(4) |
wobei 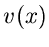 eine Funktion der zufälligen Veränderlichen
eine Funktion der zufälligen Veränderlichen 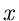 ist und aus
der Gleichung
ist und aus
der Gleichung
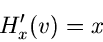 |
(5) |
bestimmt werden muß. Seien 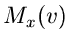 und
und
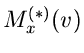 die erzeugenden
Funktionen von
die erzeugenden
Funktionen von 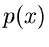 und
und 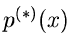 ,
,
Man kann nun zeigen, daß
mit
Rücktransformation in den Originalraum liefert die zweite verbesserte
Näherung
![\begin{displaymath}
p^{(**)}(x) = p^{(*)}(x) \left[ 1 -
\frac{5H_{x}^{(3) 2}(v)-3H_{x}^{(4)}(v) H_{x}^{(2)}(v)}{24 H_{x}^{(2) 3}(v)}
\right] ,
\end{displaymath}](img23.gif) |
(6) |
wobei wiederum 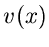 aus Gleichung (5) bestimmt werden muß.
aus Gleichung (5) bestimmt werden muß.
Dieses Verfahren läßt sich beliebig fortsetzen und liefert in jedem
Iterationsschritt eine verbesserte Näherung
Wir werden uns aber im folgenden mit der ersten (4) und der zweiten
(6) Näherung begnügen. Im allgemeinen liefert die erste Näherung
bereits hervorragende Resultate, die zweite Näherung dient dann
hauptsächlichst zur Abschätzung des Konvergenzverhaltens der Iteration.
Dieses Verfahren ist für die Simulation von Bedeutung, da, wie wir
oben erwähnt haben, die Dichtefunktion häufig nicht in analytischer
Form, sondern in Form einer der erzeugenden Funktionen bzw in Form
irgendeines Satzes ihrer Momente gegeben ist.
Beispiel.
Die einfache zentrale Normalverteilung lautete:
Die Laplace- Transformierte ist
Die logarithmisch erzeugende Funktion schließlich ist
Die logarithmischen Momente sind daher
Erhält man also bei einer Messung der höheren Momente das Ergebnis, daß
nur die beiden ersten logarithmischen Momente signifikant von Null verschieden
sind, so weiß man bereits, daß die zugehörige Dichtefunktion eine
Normalverteilung oder eine Verteilung ähnlich der Normalverteilung ist.
Zur Rücktransformation lösen wir zunächst die Bestimmungsgleichung für
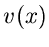 ,
,
mit der Lösung
Diesen Ausdruck setzen wir in die erste Näherung 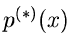 ein. Wegen
ein. Wegen
erhält man nach kurzer Rechnung
Einsetzen von 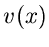 ergibt dann tatsächlich
ergibt dann tatsächlich
Bei einer Normalverteilung ergibt also die erste Näherung 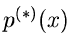 bereits das exakte Resultat. Die zweite Näherung ergibt keine Änderung,
da alle
bereits das exakte Resultat. Die zweite Näherung ergibt keine Änderung,
da alle
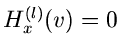 für
für 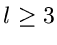 .
.
Beispiel.
Als zweites Beispiel betrachten wir die Dichtefunktion
Die logarithmisch erzeugende Funktion ist
mit den Ableitungen
Daraus ergeben sich die logarithmischen Momente
Für die Rücktransformation bestimmen wir zunächst 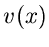 als Funktion
von
als Funktion
von 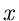 ,
,
Nach einiger Rechnung folgt die erste Näherung
Wir erkennen auf der rechten Seite die Stirlingsche Formel wieder,
sodaß wir setzen können
Wir sehen also, daß auch in diesem Fall bereits mit der ersten Näherung
die richtige Dichtefunktion erhalten wird, sofern nur 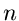 groß ist und damit
die Stirlingsche Formel angewendet werden kann.
groß ist und damit
die Stirlingsche Formel angewendet werden kann.
Die zweite Näherung ergibt:
Die Korrektur auf der rechten Seite ist hierbei aber nichts anderes als
die Korrektur der Stirlingschen Formel für kleine 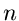 :
:
Beispiel.
Als weiteres Beispiel betrachten wir die Poisson Verteilung der diskreten
Veränderlichen 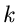 :
:
Die erzeugende Funktion ist
und die logarithmisch erzeugende Funktion wird zu
Die Ableitungen sind einfach und ergeben
Die logaritmischen Momente sind
und daher
Aus der ersten Ableitung erhalten wir
Man rechnet leicht nach, daß
und daher
Anwendung der Stirlingschen Formel ergibt dann wieder
Wir sehen also, daß auch bei diskreten Veränderlichen die erste
Näherung eine hervorragende Approximation darstellt, sofern nur
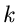 groß ist. Für kleine
groß ist. Für kleine 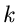 muß die zweite Näherung berechnet
werden. Dieses ergibt
muß die zweite Näherung berechnet
werden. Dieses ergibt
Dieses ist wiederum nichts anderes als die Korrektur der Stirlingschen
Formel für kleine 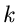 . Wir sehen aber, und darauf wollten wir in diesem
Beispiel noch einmal ausdrücklich hinweisen, daß wir in keiner Näherung
einen Wert für
. Wir sehen aber, und darauf wollten wir in diesem
Beispiel noch einmal ausdrücklich hinweisen, daß wir in keiner Näherung
einen Wert für 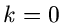 erhalten. Auch für
erhalten. Auch für 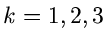 sind die Approximationen
noch ziemlich ungenau. Erst für
sind die Approximationen
noch ziemlich ungenau. Erst für 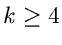 erhält man eine befriedigende
Übereinstimmung zwischen der exakten und der approximativen
Wahrscheinlichkeitsverteilung. Dieses gilt allgemein für diskrete
Veränderliche.
erhält man eine befriedigende
Übereinstimmung zwischen der exakten und der approximativen
Wahrscheinlichkeitsverteilung. Dieses gilt allgemein für diskrete
Veränderliche.
Existenz des Sattelpunkt- Verfahrens
In Formel (4) steht die zweite Ableitung 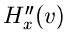 unter dem
Wurzelzeichen.
unter dem
Wurzelzeichen. 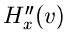 muß daher stets größer als Null sein.
Dieses zeigt man folgendermaßen. Wir drücken die logarithmisch erzeugende
Funktion durch die normale erzeugende Funktion aus:
muß daher stets größer als Null sein.
Dieses zeigt man folgendermaßen. Wir drücken die logarithmisch erzeugende
Funktion durch die normale erzeugende Funktion aus:
Wegen
finden wir
Das Integral auf der rechten Seite ist offensichtlich immer größer als
Null. Wir schließen daher:
Die zweite Ableitung 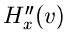 der logarithmisch erzeugenden Funktion
irgendeiner Dichtefunktion
der logarithmisch erzeugenden Funktion
irgendeiner Dichtefunktion 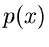 ist immer eine positiv definite Funktion.
ist immer eine positiv definite Funktion.
Weiterhin muß die Gleichung
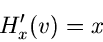 |
(7) |
mindestens eine reelle Lösung besitzen. Wir schreiben die Gleichung wieder
durch die normale erzeugende Funktion. Wegen
gilt:
Wegen (7) können wir daher auch schreiben
Einsetzen der Integraldefinition der Laplace- Transformation führt auf
Diese Gleichung ist dann und nur dann erfüllt, wenn 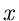 aus dem Wertebereich
der zufälligen Veränderlichen
aus dem Wertebereich
der zufälligen Veränderlichen 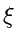 mit der Dichtefunktion
mit der Dichtefunktion 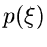 entnommen wurde. Mit anderen Worten, für alle
entnommen wurde. Mit anderen Worten, für alle 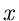 , für die die Dichtefunktion
, für die die Dichtefunktion
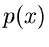 definiert ist, existiert eine Lösung der Gleichung (7).
definiert ist, existiert eine Lösung der Gleichung (7).
Dichtefunktion aus höheren Momenten
Wir nehmen an, daß alle logaritmischen Momente 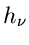 einer zufälligen
Veränderlichen
einer zufälligen
Veränderlichen 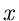 gemessen wurden. Die logarithmisch erzeugende Funktion
ist dann
gemessen wurden. Die logarithmisch erzeugende Funktion
ist dann
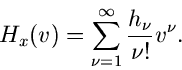 |
(8) |
Die ersten und zweiten Ableitungen sind
Wir bilden den Logarithmus der ersten Näherung des Sattelpunkts- Verfahrens,
![\begin{displaymath}
ln p^{(*)}(x) = \sum_{\nu =1}^{\infty} (1-\nu) \frac{h_{\nu}...
...\sum_{\nu =2}^{\infty}
\frac{h_{\nu}}{(\nu -2)!} v^{\nu -2}],
\end{displaymath}](img90.gif) |
(11) |
mit
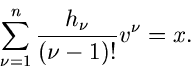 |
(12) |
Bei welchem Index 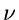 die Summenbildungen abgebrochen werden dürfen,
muß in jedem Fall einzeln entschieden werden. Zu beachten ist hierbei,
daß die zweite Ableitung stets positiv sein muß.
Das Problem bei dieser Methode besteht offensichtlich in der Lösung der
Gleichung (12), zumindest für große
die Summenbildungen abgebrochen werden dürfen,
muß in jedem Fall einzeln entschieden werden. Zu beachten ist hierbei,
daß die zweite Ableitung stets positiv sein muß.
Das Problem bei dieser Methode besteht offensichtlich in der Lösung der
Gleichung (12), zumindest für große 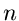 .
.
Falls die Reihen langsame Konvergenz zeigen, führt häufig folgendes
Verfahren zum Ziel. Wir setzen
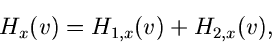 |
(13) |
wobei 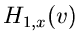 die Reihenentwicklung einer analytisch bekannten Funktion
ist.
die Reihenentwicklung einer analytisch bekannten Funktion
ist. 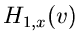 muß hierbei so gewählt werden, daß
muß hierbei so gewählt werden, daß 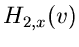 eine
schnell konvergierende Reihe wird.
eine
schnell konvergierende Reihe wird.
Beispiel.
Als Beispiel seien die folgenden logarithmischen Momente einer diskreten
Veränderlichen 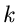 gegeben:
gegeben:
Die dritte Gleichung soll bedeuten, daß innerhalb der Meßfehler alle
höheren Momente mit dem Wert 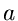 verträglich sind. Wir wissen, daß
die logarithmischen Momente der Poisson- Verteilung durch
verträglich sind. Wir wissen, daß
die logarithmischen Momente der Poisson- Verteilung durch
und die logarithmisch erzeugende Funktion durch
gegeben sind. Folglich setzen wir
Die logarithmisch erzeugende Funktion wird zu
mit den Ableitungen
Die erste Näherung des Sattelpunkt- Verfahrens lautet:
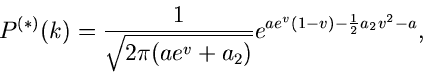 |
(14) |
mit 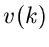 als Lösung der Gleichung
als Lösung der Gleichung
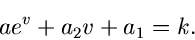 |
(15) |
Die zweite Näherung ist
Faltung von 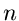 Gleichverteilungen
Gleichverteilungen
Wir hatten bereits gelernt, daß die Summe
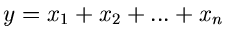 von
von 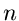 unabhängigen gleichverteilten Zufallszahlen
unabhängigen gleichverteilten Zufallszahlen 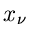 aus dem
Intervall
aus dem
Intervall
![$[-\frac{1}{2},+\frac{1}{2}]$](img118.gif) durch die logarithmisch erzeugende
Funktion
durch die logarithmisch erzeugende
Funktion
angenähert werden kann. Bei alleiniger Berücksichtigung des ersten Gliedes
der Reihe ergibt die Rücktransformation eine Normalverteilung mit
Erwartungswert 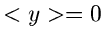 und Varianz
und Varianz
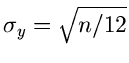 . Wir fragen
jetzt nach der Korrektur bei Berücksichtigung des zweiten Gliedes der
Reihenentwicklung. Hierzu bemerken wir, daß
. Wir fragen
jetzt nach der Korrektur bei Berücksichtigung des zweiten Gliedes der
Reihenentwicklung. Hierzu bemerken wir, daß
Die Bestimmungsgleichung für 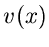 ist
ist
Einsetzen der Ableitung ergibt nach einiger Umformungen die kubische Gleichung
Diese Gleichung besitzt eine reelle und zwei komplexe Lösungen. Im folgenden
betrachten wir nur die reelle Lösung. Mit Hilfe der Cardanischen Formel
finden wir
mit
und
Die erste Näherung des Sattelpunkt- Verfahrens läßt sich dann schreiben
als
Für die zweite Näherung erhält man entsprechend
Harm Fesefeldt
2006-05-08
![]() gemessen worden sind. Dann ist die logarithmisch
erzeugende Funktion:
gemessen worden sind. Dann ist die logarithmisch
erzeugende Funktion:
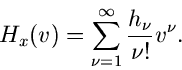
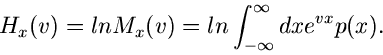
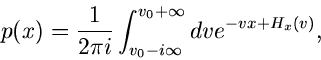
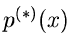 die erste Näherung des Sattelpunkt-
Verfahrens:
die erste Näherung des Sattelpunkt-
Verfahrens:
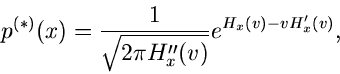
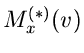 die erzeugenden
Funktionen von
die erzeugenden
Funktionen von 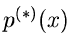 ,
,
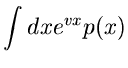
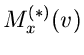
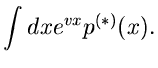
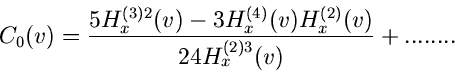
![\begin{displaymath}
p^{(**)}(x) = p^{(*)}(x) \left[ 1 -
\frac{5H_{x}^{(3) 2}(v)-3H_{x}^{(4)}(v) H_{x}^{(2)}(v)}{24 H_{x}^{(2) 3}(v)}
\right] ,
\end{displaymath}](img23.gif)
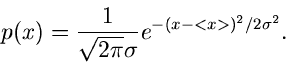
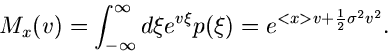
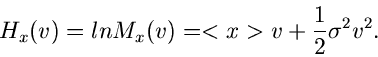
![]() ,
,
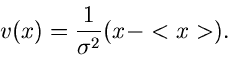
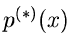 ein. Wegen
ein. Wegen
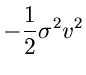
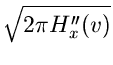
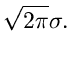
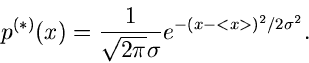
 bereits das exakte Resultat. Die zweite Näherung ergibt keine Änderung,
da alle
bereits das exakte Resultat. Die zweite Näherung ergibt keine Änderung,
da alle
 für
für 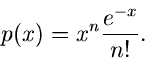
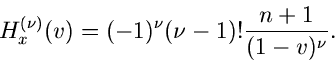
![]() als Funktion
von
als Funktion
von ![]() ,
,
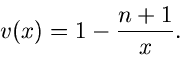
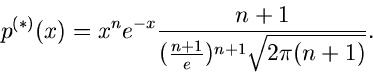
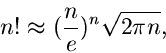
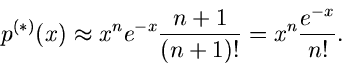
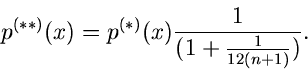
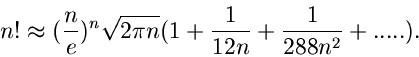
![]() :
:
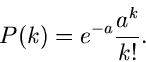
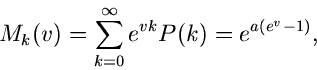
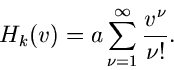
![$\displaystyle ln\left[ \frac{k}{a} \right].$](img65.gif)
![$\displaystyle (k-1) ln \left[ (\frac{a}{k})^{k} \right]$](img67.gif)
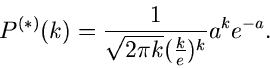
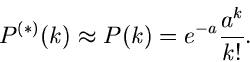
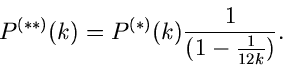
![]() unter dem
Wurzelzeichen.
unter dem
Wurzelzeichen. ![]() muß daher stets größer als Null sein.
Dieses zeigt man folgendermaßen. Wir drücken die logarithmisch erzeugende
Funktion durch die normale erzeugende Funktion aus:
muß daher stets größer als Null sein.
Dieses zeigt man folgendermaßen. Wir drücken die logarithmisch erzeugende
Funktion durch die normale erzeugende Funktion aus:
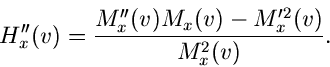
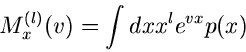
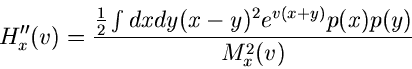
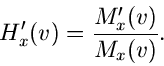
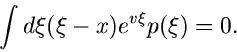
![]() einer zufälligen
Veränderlichen
einer zufälligen
Veränderlichen ![]() gemessen wurden. Die logarithmisch erzeugende Funktion
ist dann
gemessen wurden. Die logarithmisch erzeugende Funktion
ist dann
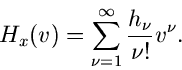
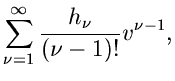
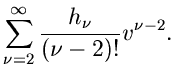
![\begin{displaymath}
ln p^{(*)}(x) = \sum_{\nu =1}^{\infty} (1-\nu) \frac{h_{\nu}...
...\sum_{\nu =2}^{\infty}
\frac{h_{\nu}}{(\nu -2)!} v^{\nu -2}],
\end{displaymath}](img90.gif)
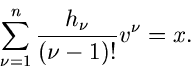
![]() gegeben:
gegeben:
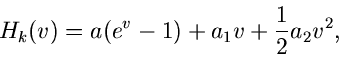
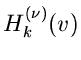
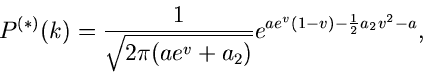
![\begin{displaymath}
P^{(**)}(k) = P^{(*)}(k) \left[ 1 -
\frac{ae^{v} (2 ae^{v} -3 a_{2})}{24 (ae^{v}+ a_{2})^{3}} \right] .
\end{displaymath}](img115.gif)
![]() Gleichverteilungen
Gleichverteilungen ![]() von
von ![]() unabhängigen gleichverteilten Zufallszahlen
unabhängigen gleichverteilten Zufallszahlen ![]() aus dem
Intervall
aus dem
Intervall
![$[-\frac{1}{2},+\frac{1}{2}]$](img118.gif) durch die logarithmisch erzeugende
Funktion
durch die logarithmisch erzeugende
Funktion
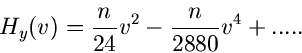
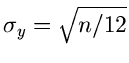 . Wir fragen
jetzt nach der Korrektur bei Berücksichtigung des zweiten Gliedes der
Reihenentwicklung. Hierzu bemerken wir, daß
. Wir fragen
jetzt nach der Korrektur bei Berücksichtigung des zweiten Gliedes der
Reihenentwicklung. Hierzu bemerken wir, daß
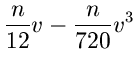
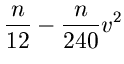
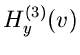
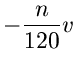
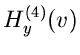
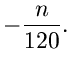
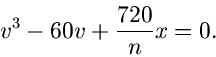
![\begin{displaymath}
v_{1,2}(x) = \sqrt[3]{-q \pm \sqrt{q^{2}+p^{3}}}
\end{displaymath}](img133.gif)
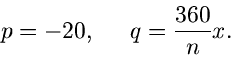
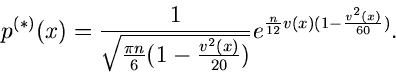
![\begin{displaymath}
p^{(**)}(x) = p^{(*)}(x) \left[ 1 -
\frac{3-\frac{13}{20} v^{2}(x)}{20n(1-\frac{v^{2}(x)}{20})^{3}} \right] .
\end{displaymath}](img136.gif)