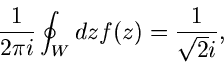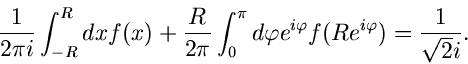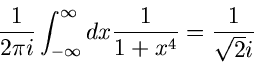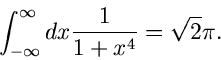Komplexe Funktionen
Komplexe Zahlen
Die formale Definition der imaginären Einheit 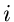 mit Hilfe der Definition
mit Hilfe der Definition
 |
(1) |
führt zu einer Erweiterung des Zahlenbegriffs, zu den komplexen Zahlen.
Mit Hilfe dieser Definition können wir die Wurzeln der algebraischen
Gleichung
angeben zu
Eine komplexe Zahl besitzt die allgemeine Form
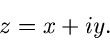 |
(2) |
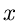 nennt man den Realteil,
nennt man den Realteil, 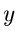 den Imaginärteil von
den Imaginärteil von 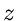 und schreibt
und schreibt
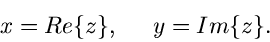 |
(3) |
Man veranschaulicht komplexe Zahlen durch Punkte in der Gaußschen
Zahlenebene (siehe Abb.1).
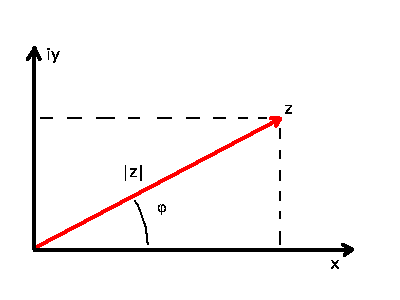
Abbildung 1:
Darstellung einer komplexen Zahl in der Ebene.
Der Betrag der komplexen Zahl ist
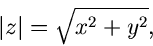 |
(4) |
sodaß wir 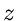 auch in der trigonometrischen Form
auch in der trigonometrischen Form
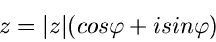 |
(5) |
schreiben können. Den Winkel 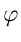 nennt man das Argument der komplexen
Zahl
nennt man das Argument der komplexen
Zahl 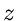 . Aus den Reihenentwicklungen für
. Aus den Reihenentwicklungen für 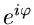 ,
, 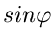 und
und
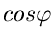 kann man die Eulersche Formel
kann man die Eulersche Formel
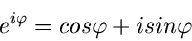 |
(6) |
herleiten. Daraus folgt die Exponentialform der komplexen Zahlen
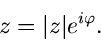 |
(7) |
Aus der trigonometrischen Darstellung ersieht man, daß das Argument 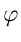 nicht eindeutig ist. Für eine gegebene komplexe Zahl besitzt das
Argument unendlich viele Werte. Unter dem Hauptwert des Arguments versteht
man den Wert zwischen
nicht eindeutig ist. Für eine gegebene komplexe Zahl besitzt das
Argument unendlich viele Werte. Unter dem Hauptwert des Arguments versteht
man den Wert zwischen 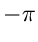 und
und 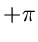 .
.
Grundoperationen.
Die Grundoperationen können aus den Grundoperationen der Real- und
Imaginärteile hergeleitet werden.
Bei der Multiplikation und Division wählt man besser die Exponentialform:
Die Rechenregeln für komplexe Zahlen sind so definiert, daß alle
vom Rechnen mit reellen Zahlen her bekannten Regeln und Relationen
(Kommutativität, Distributivität, u.s.w.) erhalten bleiben. Lediglich die
Ordnungsrelationen (
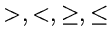 ) haben für komplexe Zahlen selbst keine
Bedeutung, sondern nur für die Beträge der komplexen Zahlen. Die
wichtigsten Ungleichungen seien im folgenden zusammengestellt.
) haben für komplexe Zahlen selbst keine
Bedeutung, sondern nur für die Beträge der komplexen Zahlen. Die
wichtigsten Ungleichungen seien im folgenden zusammengestellt.
Die zu 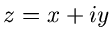 konjugiert komplexe Zahl
konjugiert komplexe Zahl 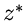 ist durch
ist durch
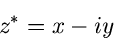 |
(15) |
gegeben. Die folgenden einfachen Rechenregeln lassen sich leicht
nachrechnen.
Gebiete und Wege
Irgendeine Teilmenge der komplexen Zahlenebene heißt ein Gebiet
G. Die Punkte auf dem Rand gehören nicht mit zum Gebiet. Daher sagt man
spezieller offenes Gebiet oder nicht abgeschlossenes Gebiet.
Bei einem abgeschlossenen Gebiet dagegen zählt der Rand mit zum Gebiet.
Gebiete können beschränkt oder unbeschränkt sein, je nachdem ob die
Zahl 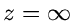 mit zum Gebiet zählt oder nicht. Mathematisch exakter
ausgedrückt sagt man, ein Gebiet ist beschränkt, wenn sich eine (reelle)
Zahl
mit zum Gebiet zählt oder nicht. Mathematisch exakter
ausgedrückt sagt man, ein Gebiet ist beschränkt, wenn sich eine (reelle)
Zahl 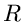 angeben läßt, sodaß
angeben läßt, sodaß
Gebiete können einfach oder mehrfach zusammenhängend sein, je nachdem wie
groß die Anzahl der geschlossenen Ränder des Gebietes ist (siehe Abb.2).
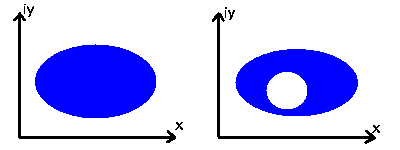
Abbildung 2:
Einfach- und zweifach zusammenhängendes Gebiet.
Einen Weg in der komplexen Zahlenebene kann man durch die
Parameterdarstellung
![\begin{displaymath}
z(t) = x(t) + iy(t), \; \; \; t \in [t_{1}.t_{2}], \; \; t \in R,
\end{displaymath}](img44.gif) |
(16) |
beschreiben. Alle auf einem Kreis liegenden Zahlen 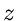 kann man durch die
Gleichung
kann man durch die
Gleichung
beschreiben. Hierbei ist
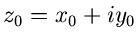 der Mittelpunkt und
der Mittelpunkt und 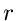 der Radius des Kreises.
der Radius des Kreises.
Geraden, parallel zur 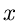 - bzw
- bzw 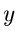 - Achse, werden durch
- Achse, werden durch
beschrieben. Hierin sind die rein reellen und rein imaginären Zahlen mit
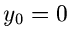 bzw
bzw 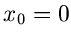 enthalten.
enthalten.
Funktionen
Ähnlich wie in der reellen Analysis durch eine Funktion einem 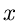 - Wert
ein bestimmter
- Wert
ein bestimmter 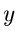 - Wert zugeordnet wird,
- Wert zugeordnet wird, 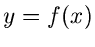 , so definiert man im
Komplexen eine Zuordnung einer komplexen
, so definiert man im
Komplexen eine Zuordnung einer komplexen 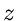 - Ebene auf eine komplexe
- Ebene auf eine komplexe
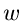 - Ebene. Jedem Punkt
- Ebene. Jedem Punkt 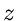 wird durch
wird durch 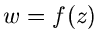 eine Zahl
eine Zahl  zugeordnet (siehe Abb.3).
zugeordnet (siehe Abb.3).
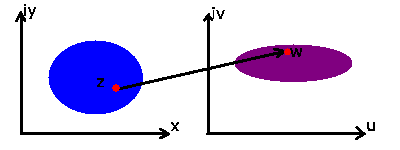
Abbildung 3:
Darstellung einer komplexen Funktion in der z- und w- Ebene.
Man schreibt dieses auch häufig in der Form
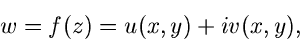 |
(17) |
wobei 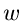 natürlich, wie auch
natürlich, wie auch 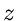 , einen Real- und Imaginärteil,
nämlich
, einen Real- und Imaginärteil,
nämlich 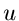 und
und 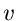 , haben muß.
, haben muß.
Stetigkeit und Differenzierbarkeit der Funktion  im Punkte
im Punkte  wird ähnlich wie im Reellen durch die Existenz der Grenzwerte
wird ähnlich wie im Reellen durch die Existenz der Grenzwerte
erklärt. Wie im Reellen gelten die Differentiationsregeln
Existiert 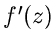 für alle
für alle 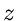 aus einem Gebiet G, so heißt
aus einem Gebiet G, so heißt  in
G regulär, analytisch oder holomorph. Solche Punkte
in
G regulär, analytisch oder holomorph. Solche Punkte 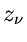 , an denen
, an denen
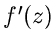 nicht existiert, nennt man singuläre Stellen. Es kann natürlich
vorkommen, daß
nicht existiert, nennt man singuläre Stellen. Es kann natürlich
vorkommen, daß  in einem ganzen Gebiet nicht regulär ist. Mit
solchen Funktionen werden wir uns aber nicht beschäftigen. Die in unseren
Anwendungen vorkommenden Funktionen sind in der gesamten Zahlenebene
regulär, bis auf endlich oder unenedlich viele singuläre Punkte.
in einem ganzen Gebiet nicht regulär ist. Mit
solchen Funktionen werden wir uns aber nicht beschäftigen. Die in unseren
Anwendungen vorkommenden Funktionen sind in der gesamten Zahlenebene
regulär, bis auf endlich oder unenedlich viele singuläre Punkte.
Die Grenzwerte (18) und (19) müssen für alle möglichen, unendlich
vielen, Annäherungen des Punktes 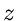 nach
nach  existieren und
identisch gleich sein. Diese Forderung führt zu einer starken
Verschärfung des Differentiationsbegriffes in der komplexen Ebene
verglichen mit der auf der reellen Zahlengeraden. Wir diskutieren die
Grenzwerte auf zwei Wegen, nämlich Weg I parallel zur reellen Achse
und Weg II parallel zur imaginären Achse (siehe Abb.4).
existieren und
identisch gleich sein. Diese Forderung führt zu einer starken
Verschärfung des Differentiationsbegriffes in der komplexen Ebene
verglichen mit der auf der reellen Zahlengeraden. Wir diskutieren die
Grenzwerte auf zwei Wegen, nämlich Weg I parallel zur reellen Achse
und Weg II parallel zur imaginären Achse (siehe Abb.4).
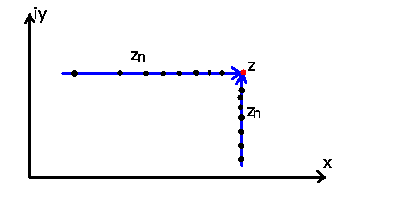
Abbildung 4:
Zur Ableitung der Cauchy Riemannschen Differentialgleichung.
Auf Weg I ist 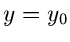 und somit
und somit
Auf Weg II gilt entsprechend mit 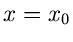
Beide Grenzwerte müssen identisch gleich sein. Da auch Real- und Imaginärteil
getrennt gleich sein müssen, gelten die wichtigen Cauchy- Riemannschen
Differentialgleichungen
Nur und nur dann, wenn diese Gleichungen erfüllt sind, ist die Funktion
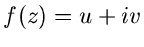 regulär. Oder, anders ausgedrückt, wenn einer der beiden,
Realteil
regulär. Oder, anders ausgedrückt, wenn einer der beiden,
Realteil 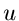 oder Imaginärteil
oder Imaginärteil 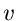 , bekannt sind, läßt sich der andere
Teil daraus berechnen.
, bekannt sind, läßt sich der andere
Teil daraus berechnen.
Differenziert man die Cauchy- Riemannschen Differentialgleichungen ein
zweites mal (die Existenz der Ableitungen vorausgesetzt), so erhält man
die Laplaceschen Differentialgleichungen
Wie wir später noch ausführen werden, folgt aus der Existenz der ersten
Ableitung 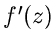 bereits die Existenz aller höheren Ableitungen
bereits die Existenz aller höheren Ableitungen
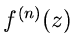 . Daher sind die Laplaceschen Differentialgleichungen
weitere notwendige Bedingungen, die
. Daher sind die Laplaceschen Differentialgleichungen
weitere notwendige Bedingungen, die 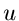 und
und 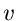 getrennt erfüllen
müssen, um Real- und Imaginärteil einer regulären Funktion sein zu
können. Eine Lösung der Laplaceschen Differentialgleichung heißt
harmonische Funktion. Mit dieser Definition gilt: Real- und Imaginärteil
einer regulären Funktion
getrennt erfüllen
müssen, um Real- und Imaginärteil einer regulären Funktion sein zu
können. Eine Lösung der Laplaceschen Differentialgleichung heißt
harmonische Funktion. Mit dieser Definition gilt: Real- und Imaginärteil
einer regulären Funktion  sind harmonische Funktionen.
Unter einer ganzen Funktion versteht man eine Funktion, die, abgesehen
von einer Singularität im Unendlichen, in der ganzen
sind harmonische Funktionen.
Unter einer ganzen Funktion versteht man eine Funktion, die, abgesehen
von einer Singularität im Unendlichen, in der ganzen 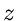 - Ebene
regulär ist.
- Ebene
regulär ist.
Im folgenden sollen die für die Anwendungen wichtigsten Funktionen
kurz erläutert werden. Es sind dieses die ganzen rationalen Funktionen,
die gebrochenen rationalen Funktionen, die Potenz- und Wurzelfunktion,
die Exponentialfunktion sowie die trigonometrischen Funktionen.
Ganze rationale Funktionen.
Die ganzen rationalen Funktionen oder Polynome
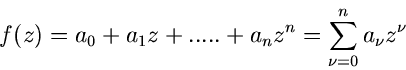 |
(26) |
sind in der ganzen 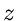 - Ebene regulär und daher beliebig oft differenzierbar.
Offensichtlich ist sogar
- Ebene regulär und daher beliebig oft differenzierbar.
Offensichtlich ist sogar
Ein Wert 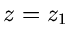 , für den
, für den  verschwindet, also den Wert
verschwindet, also den Wert 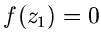 annimmt, heißt Nullstelle von
annimmt, heißt Nullstelle von  . Ein Polynom
. Ein Polynom 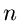 -ter Ordnung hat genau
-ter Ordnung hat genau
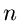 Nullstellen
Nullstellen
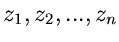 . Daher kann man Polynome auch in der
Produktform
. Daher kann man Polynome auch in der
Produktform
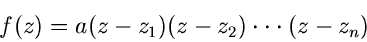 |
(27) |
schreiben. Die Nullstellen 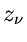 brauchen nicht alle verschieden zu sein.
Allgemeiner kann eine Nullstelle mehrfach (
brauchen nicht alle verschieden zu sein.
Allgemeiner kann eine Nullstelle mehrfach (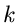 -fach) auftreten, d.h. von
der Ordnung
-fach) auftreten, d.h. von
der Ordnung 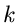 sein. Hat also das Polynom
sein. Hat also das Polynom 
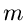 verschiedene
Nullstellen mit den Ordnungen
verschiedene
Nullstellen mit den Ordnungen
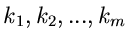 , so können wir auch
schreiben
, so können wir auch
schreiben
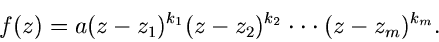 |
(28) |
Durch ihre Nullstellen und deren Ordnung ist eine ganze rationale Funktion
also bis auf einen konstanten Faktor vollständig festgelegt. Man
charakterisiert daher ganze rationale Funktionen durch das sogenannte
Nullstellendiagramm (Abb.5).
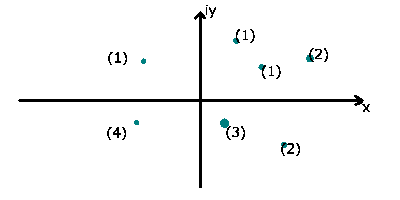
Abbildung 5:
Nullstellen Diagramm einer ganzen rationalen Funktion.
Hierbei werden die Nullstellen in der komplexen Ebene mit Hilfe kleiner
Kreise (Nullen) eingezeichnet und deren Ordnungen in Klammern beigefügt.
Gebrochene rationale Funktionen.
Gebrochene rationale Funktionen
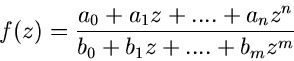 |
(29) |
können ähnlich wie ganze rationale Funktionen charakterisiert werden. Man
muß nur die Nullstellen vom Zähler- und Nennerpolynom getrennt
bestimmen und erhält die Produktform
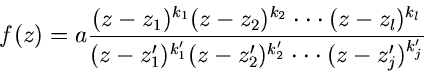 |
(30) |
Hierbei sind also
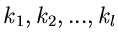 die Ordnungen der
die Ordnungen der 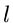 verschiedenen
Nullstellen
verschiedenen
Nullstellen
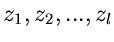 des Zählerpolynoms und
des Zählerpolynoms und
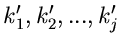 die Ordnungen der
die Ordnungen der 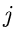 Nullstellen
Nullstellen
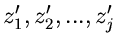 des Nennerpolynoms. Die Nullstellen des
Nennerpolynoms sind nun aber singuläre Stellen der Funktion
des Nennerpolynoms. Die Nullstellen des
Nennerpolynoms sind nun aber singuläre Stellen der Funktion  .
Man nennt daher eine
.
Man nennt daher eine 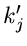 -fache Nullstelle des Nennerpolynoms einen
Pol
-fache Nullstelle des Nennerpolynoms einen
Pol 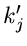 -facher Ordnung der Funktion
-facher Ordnung der Funktion  . Das
Pol- Nullstellen- Diagramm ist genauso wie für ganze rationale Funktionen
definiert, nur daß zusätzlich die Pole durch kleine Kreuze gekennzeichnet
werden (Abb.6).
. Das
Pol- Nullstellen- Diagramm ist genauso wie für ganze rationale Funktionen
definiert, nur daß zusätzlich die Pole durch kleine Kreuze gekennzeichnet
werden (Abb.6).
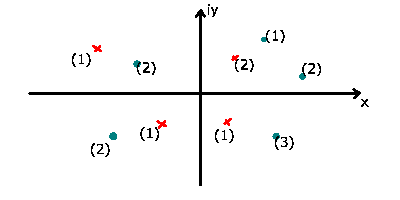
Abbildung 6:
Pol- Nullstellen Diagramm einer rationalen Funktion.
Vorsicht ist geboten, wenn eine Nullstelle  des Nennerpolynoms
gleich einer Nullstelle
des Nennerpolynoms
gleich einer Nullstelle  des Zählerpolynoms ist. In diesem Fall
entspricht das Verhalten der Funktion
des Zählerpolynoms ist. In diesem Fall
entspricht das Verhalten der Funktion  für
für 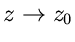 dem der
Funktion
dem der
Funktion
wobei 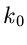 und
und 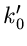 die Ordnungen der gemeinsamen Nullstelle
die Ordnungen der gemeinsamen Nullstelle  vom
Zähler- und Nennerpolynom sind. Ist also
vom
Zähler- und Nennerpolynom sind. Ist also 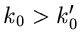 , so hat
, so hat  in
in  eine Nullstelle der Ordnung
eine Nullstelle der Ordnung 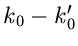 , ist umgekehrt
, ist umgekehrt
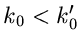 , so hat f(z) einen Pol der Ordnung
, so hat f(z) einen Pol der Ordnung 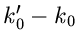 . Ist
. Ist
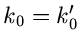 , so ist die Funktion
, so ist die Funktion  in
in  ungleich 0 und
regulär. Wir erinnern in diesem Zusammenhang an die nützliche Regel
von L'Hopital, die man in der Form
ungleich 0 und
regulär. Wir erinnern in diesem Zusammenhang an die nützliche Regel
von L'Hopital, die man in der Form
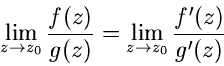 |
(31) |
schreiben kann. Diese Formel erlaubt die Untersuchung des
Grenzwertverhaltens von Quotienten beliebiger Funktionen  und
und 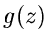 .
.
Von Interesse ist noch das Verhalten der Funktion  im Unendlichen.
Der Funktion
im Unendlichen.
Der Funktion  wird für
wird für 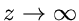 das Verhalten zugeordnet,
daß die Funktion
das Verhalten zugeordnet,
daß die Funktion
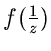 für
für 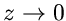 zeigt. Danach können
ganze rationale Funktionen wie auch gebrochene rationale Funktionen im
Unendlichen regulär sein, einen mehrfachen Pol oder eine mehrfache
Nullstelle besitzen.
zeigt. Danach können
ganze rationale Funktionen wie auch gebrochene rationale Funktionen im
Unendlichen regulär sein, einen mehrfachen Pol oder eine mehrfache
Nullstelle besitzen.
Die Funktion
hat in 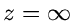 eine einfache Nullstelle, da
eine einfache Nullstelle, da
und die Funktion
in 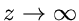 einen dreifachen Pol, da
einen dreifachen Pol, da
Potenz- und Wurzelfunktion.
Die mehrfache Multiplikation ein und derselben Zahl 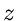 führt zur
Potenzfunktion,
führt zur
Potenzfunktion,
Dieses ist offensichtlich eine spezielle ganze rationale Funktion.
Die Umkehrung dieser Fragestellung, nämlich die Zahl 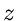 , deren
, deren
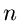 -te Potenz die Zahl
-te Potenz die Zahl 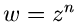 ergibt, führt auf den Begriff der
Wurzel,
ergibt, führt auf den Begriff der
Wurzel,
Wie wir am Anfang dieses Kapitels bereits ausgeführt haben, ist die
Exponentialfunktion nicht eindeutig, vielmehr ergeben sich 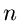 Lösungen
Lösungen
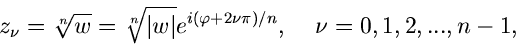 |
(32) |
deren 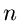 -te Potenz alle die Zahl
-te Potenz alle die Zahl 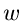 ergeben.
ergeben.
Exponentialfunktion und trigonometrische Funktionen.
Die Exponentialfunktion ist mittels der Reihenentwicklung
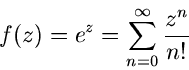 |
(33) |
definiert. Diese Funktion ist in der gesamten 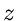 - Ebene (bis auf
- Ebene (bis auf 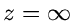 )
regulär und nullstellenfrei. Mit Hilfe der Eulerschen Formel ergibt sich
)
regulär und nullstellenfrei. Mit Hilfe der Eulerschen Formel ergibt sich
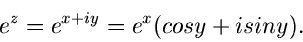 |
(34) |
Damit läßt sich also die komplexe Funktion 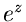 mit Hilfe der
reellen Funktionen
mit Hilfe der
reellen Funktionen 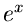 ,
, 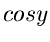 und
und 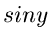 schreiben. Man bestätigt
leicht die folgenden Regeln
schreiben. Man bestätigt
leicht die folgenden Regeln
Die letzte Formel zeigt, daß die Funktion 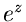 periodisch auf Parallelen
zur reellen Achse ist.
periodisch auf Parallelen
zur reellen Achse ist.
Die trigonometrischen Funktionen werden über die Relationen
definiert. Alle diese Funktionen besitzen eine singuläre Stelle im
Unendlichen und sind sonst regulär. Die Funktionen 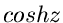 und
und 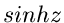 besitzen auf der imaginären Achse unendlich viele Nullstellen in
äquidistanten Abständen, während die Funktionen
besitzen auf der imaginären Achse unendlich viele Nullstellen in
äquidistanten Abständen, während die Funktionen 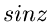 und
und 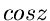 außer den bekannten Nullstellen auf der reellen Achse keine weiteren
Nullstellen besitzen. Die hieraus abgeleiteten Funktionen
außer den bekannten Nullstellen auf der reellen Achse keine weiteren
Nullstellen besitzen. Die hieraus abgeleiteten Funktionen 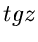 und
und
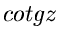 werden wie im Reellen durch die Quotienten von
werden wie im Reellen durch die Quotienten von 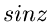 und
und
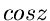 ausgedrückt. Diese Funktionen besitzen daher Pole auf der reellen
Achse. Die Ordnung dieser Pole werden wir später diskutieren.
ausgedrückt. Diese Funktionen besitzen daher Pole auf der reellen
Achse. Die Ordnung dieser Pole werden wir später diskutieren.
Linienintegral
Gegeben sei ein Weg 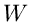 in der komplexen Ebene, dargestellt in der
Parameterform
in der komplexen Ebene, dargestellt in der
Parameterform
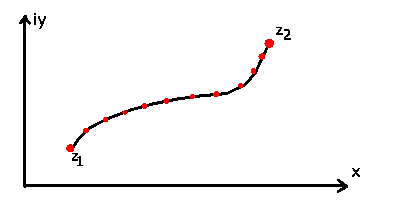
Abbildung 7:
Integral in der komplexen Ebene.
Das Linienintegral von  längs des Weges
längs des Weges 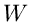 ist dann definiert als
ist dann definiert als
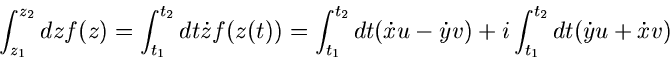 |
(39) |
mit
Da das Integral in der komplexen 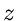 - Ebene auf zwei reelle Integrale
zurückgeführt wurde, gelten formal die gleichen Regeln wie im Reellen:
- Ebene auf zwei reelle Integrale
zurückgeführt wurde, gelten formal die gleichen Regeln wie im Reellen:
Handelt es sich bei dem Weg um einen vollständigen Kreis mit dem Radius
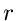 und dem Mittelpunkt
und dem Mittelpunkt
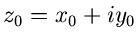 (der Parameter
(der Parameter 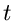 ist durch
ist durch
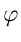 ersetzt),
ersetzt),
so ergibt sich das Linienintegral
Allgemeiner nennt man jedes Linienintegral über eine geschlossene Kurve
ein Kreisintegral (Abb.8).
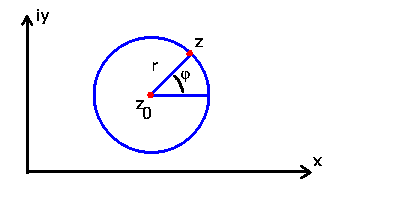
Abbildung 8:
Integration auf einem Kreisweg.
Beispiel.
Sei speziell
dann ergibt sich für das Kreisintegral um  mit Radius
mit Radius 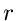
oder
Dieses deutet bereits eines der wichtigsten und bemerkenswertesten Ergebnisse
der Funktionentheorie an. Das Kreisintegral der Funktion
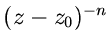 hängt nicht vom Radius
hängt nicht vom Radius 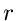 und vom Kreismittelpunkt
und vom Kreismittelpunkt  ab. Es ist
für jeden Kreis und an jedem Ort der komplexen Ebene gleich groß.
Offensichtlich kommt es hierbei noch nicht einmal darauf an, ob es wirklich
ein Kreis ist. Die obige Aussage kann dahingehend verallgemeinert werden,
daß es sich um einen geschlossenen Weg in der komplexen
ab. Es ist
für jeden Kreis und an jedem Ort der komplexen Ebene gleich groß.
Offensichtlich kommt es hierbei noch nicht einmal darauf an, ob es wirklich
ein Kreis ist. Die obige Aussage kann dahingehend verallgemeinert werden,
daß es sich um einen geschlossenen Weg in der komplexen 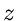 - Ebene handeln
muß. Es sind dieses besonders die Kreisintegrale, die uns im folgenden
beschäftigen werden.
- Ebene handeln
muß. Es sind dieses besonders die Kreisintegrale, die uns im folgenden
beschäftigen werden.
Hauptsatz der Funktionentheorie
Die Verallgemeinerung dieses Sachverhaltes wird im Hauptsatz der
Funktionentheorie folgendermaßen formuliert:
Satz: Ist  in einem einfach zusammenhängenden Gebiet G regulär,
dann ist
in einem einfach zusammenhängenden Gebiet G regulär,
dann ist
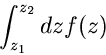 |
(45) |
unabhängig vom Weg W, der die beiden Punkte 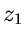 und
und 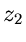 verbindet,
oder, was das gleiche ist, auf einem geschlossenen Weg gilt
verbindet,
oder, was das gleiche ist, auf einem geschlossenen Weg gilt
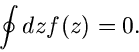 |
(46) |
Der geschlossene Weg muß dabei natürlich ganz in G liegen, er darf
insbesondere keine singulären Stellen der Funktion  umschließen.
umschließen.
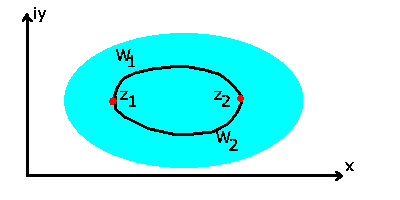
Abbildung 9:
Zum Hauptsatz der Funktionentheorie.
Stammfunktion.
Gegeben sei eine Funktion  , die in einem Gebiet
, die in einem Gebiet 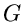 regulär ist.
Die Funktion
regulär ist.
Die Funktion
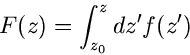 |
(47) |
ist dann, wie wir jetzt wissen, unabhängig von dem Weg von  nach
nach
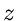 , auf dem das Integral berechnet wird, wenn nur der Weg ganz in
, auf dem das Integral berechnet wird, wenn nur der Weg ganz in 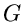 verläuft, einschließlich des Startwertes
verläuft, einschließlich des Startwertes  . Wie man zeigen kann,
ist
. Wie man zeigen kann,
ist 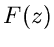 dann ebenfalls eine reguläre Funktion in
dann ebenfalls eine reguläre Funktion in 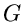 und es gilt
und es gilt
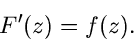 |
(48) |
Man nennt 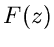 die Stammfunktion von
die Stammfunktion von  . Ist
. Ist 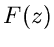 bekannt, kann das
Integral über
bekannt, kann das
Integral über  von
von 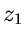 bis
bis 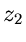 berechnet werden gemäß
berechnet werden gemäß
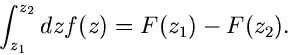 |
(49) |
Folgerungen.
Ein wichtiges Beispiel für die Anwendungen des Hauptsatzes ist das folgende.
Gegeben sei ein zweifach zusammenhängendes Gebiet G, in dem  regulär
ist. In dem unschraffierten Bereich braucht
regulär
ist. In dem unschraffierten Bereich braucht  nicht regulär zu sein,
es können dort singuläre Stellen liegen (Abb.10).
nicht regulär zu sein,
es können dort singuläre Stellen liegen (Abb.10).
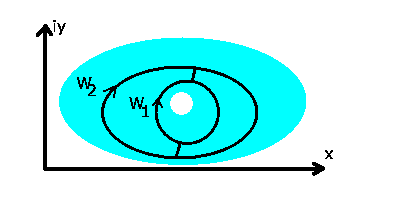
Abbildung 10:
Folgerungen aus dem Hauptsatz der Funktionentheorie.
Für die Integrale auf den beiden geschlossenen Wegen  und
und  können wir zunächst nichts aussagen, da das Gebiet G nicht einfach
zusammenhängend ist, wir den Hauptsatz also nicht anwenden können.
Wir können
können wir zunächst nichts aussagen, da das Gebiet G nicht einfach
zusammenhängend ist, wir den Hauptsatz also nicht anwenden können.
Wir können 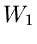 und
und 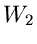 aber in zwei andere Kurven
aber in zwei andere Kurven 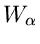 und
und 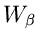 zerlegen, wie in der folgenden Skizze dargestellt (Abb.11).
zerlegen, wie in der folgenden Skizze dargestellt (Abb.11).
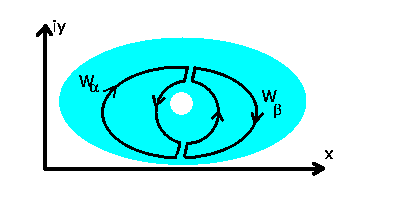
Abbildung 11:
Aufteilung des Integrationsweges.
Auf den beiden Verbindungswegen heben sich die Integrale offensichtlich
gegenseitig auf, sodaß gilt
Im Inneren der geschlossenen Wege 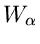 und
und 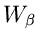 ist
ist  jedoch regulär, also nach dem Hauptsatz sind die beiden Integrale
auf der linken Seite der Gleichung identisch gleich Null. Daher gilt auch
jedoch regulär, also nach dem Hauptsatz sind die beiden Integrale
auf der linken Seite der Gleichung identisch gleich Null. Daher gilt auch
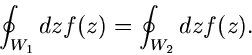 |
(50) |
Der Wert des Integrals hängt also nicht von der speziellen Form des den
singulären Innenbereiches umfassenden Weges ab.
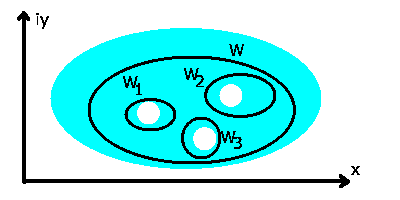
Abbildung 12:
Integration in einem mehrfach zusammenhängendem Gebiet.
Man kann diesen Sachverhalt noch verschärfen. Der Weg 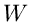 möge
möge 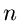 singuläre Bereiche (Stellen) einschließen,
dann gilt:
singuläre Bereiche (Stellen) einschließen,
dann gilt:
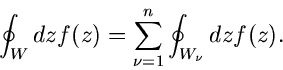 |
(51) |
In einem mehrfach zusammenhängenden Gebiet G, in dem  regulär ist,
hängt der Wert des auf einem geschlossenen Weg gebildeten Integrals
regulär ist,
hängt der Wert des auf einem geschlossenen Weg gebildeten Integrals
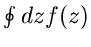 nur davon ab, welche der singulären Bereiche (Stellen)
vom Integrationsweg umschlossen werden (Abb. 12).
nur davon ab, welche der singulären Bereiche (Stellen)
vom Integrationsweg umschlossen werden (Abb. 12).
Integralformel von Cauchy.
Wir betrachten weiter das Integral
 sei im gesamten Gebiet G regulär. Die unterm Integral stehende Funktion
hat dann einen einfachen Pol im Punkte
sei im gesamten Gebiet G regulär. Die unterm Integral stehende Funktion
hat dann einen einfachen Pol im Punkte  , dargestellt als Kreuz in der
folgenden Skizze (Abb.13).
, dargestellt als Kreuz in der
folgenden Skizze (Abb.13).
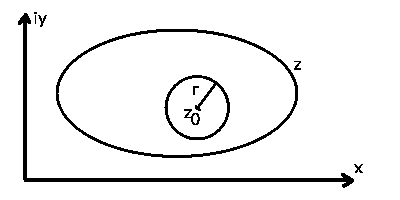
Abbildung 13:
Zur Integralformel von Chauchy.
Wir bilden das Integral auf einem Kreis mit Radius 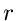 um den Mittelpunkt
um den Mittelpunkt
 ,
,
Für 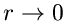 , also bei stetiger Verkleinerung des Kreisradius, erhalten
wir
, also bei stetiger Verkleinerung des Kreisradius, erhalten
wir
Andererseits wissen wir aus Formel (50), daß der Wert des links
stehenden Integrals nicht vom Radius des Kreises abhängt, wir können also
allgemein schreiben:
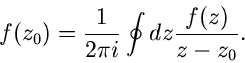 |
(52) |
Dieses ist wieder eine bemerkenswerte Formel, die wir noch kurz interpretieren
wollen. Der Hauptinhalt liegt darin, daß sich mit ihrer Hilfe alle
Funktionswerte 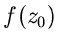 im Innern einer geschlossenen Kurve berechnen
lassen, wenn nur die Funktionswerte
im Innern einer geschlossenen Kurve berechnen
lassen, wenn nur die Funktionswerte  auf der Kurve selbst bekannt sind.
auf der Kurve selbst bekannt sind.
Formel (52) kann in folgender Form verallgemeinert werden. Sei  eine
bis auf endlich viele singuläre Stellen
eine
bis auf endlich viele singuläre Stellen
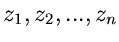 reguläre Funktion. Sei
reguläre Funktion. Sei  insbesondere im Unendlichen für
insbesondere im Unendlichen für
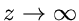 regulär. Wir bilden das Integral
regulär. Wir bilden das Integral
wobei der Weg 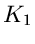 alle Singularitäten umschließt und
alle Singularitäten umschließt und  jetzt
aber, im Gegensatz zur normalen Integralformel von Cauchy, außerhalb
des von
jetzt
aber, im Gegensatz zur normalen Integralformel von Cauchy, außerhalb
des von 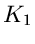 gebildeten Ringebietes liegt.
gebildeten Ringebietes liegt.
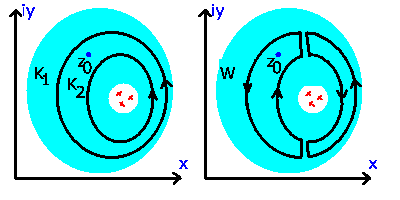
Abbildung 14:
Zur Integralformel von Chauchy.
Ein zweiter geschlossener Weg 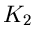 möge darüber hinaus auch noch
möge darüber hinaus auch noch
 einschließen. Wir schneiden das Ringgebiet in gewohnter Weise
auf und bilden das Integral auf dem von
einschließen. Wir schneiden das Ringgebiet in gewohnter Weise
auf und bilden das Integral auf dem von 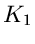 ,
, 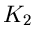 und den beiden
Verbindungslinien gebildeten Weges
und den beiden
Verbindungslinien gebildeten Weges 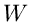 . Für diesen Weg kann die Formel
(52) angewendet werden, da
. Für diesen Weg kann die Formel
(52) angewendet werden, da  jetzt innerhalb des geschlossenen
Weges
jetzt innerhalb des geschlossenen
Weges 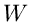 liegt, und
liegt, und  in diesem Gebiet regulär ist.
in diesem Gebiet regulär ist.
In bekannter Weise kann dieses Integral umgeschrieben werden zu
Das Kreisintegral über 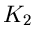 ist aber unabhängig vom Weg, siehe (51). Vergrößern
wir den Radius
ist aber unabhängig vom Weg, siehe (51). Vergrößern
wir den Radius 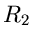 dieses Weges bis nach
dieses Weges bis nach
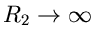 , so
verschwindet das Integral über
, so
verschwindet das Integral über 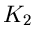 wegen der Regularität von
wegen der Regularität von  für
für 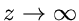 . Daher gilt
. Daher gilt
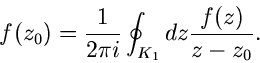 |
(53) |
Die Integralformel von Cauchy gilt also auch für das Außengebiet eines
geschlossenen Weges, wenn die Funktion  dort überall regulär ist,
einschließlich
dort überall regulär ist,
einschließlich 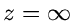 .
.
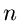 -malige Differentiation liefert
-malige Differentiation liefert
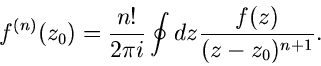 |
(54) |
Dieses ist der Beweis dafür, daß eine einmal differenzierbare Funktion
beliebig oft differenzierbar ist.
Laurent- Reihe
Betrachten wir nun in der komplexen Ebene ein gewisses Gebiet um den Punkt
 herum. Wenn die Funktion
herum. Wenn die Funktion  in
in  regulär ist, gilt
die Reihenentwicklung
regulär ist, gilt
die Reihenentwicklung
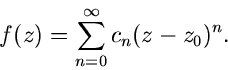 |
(55) |
Dieses sind Reihenentwicklungen, wie wir sie schon aus der reellen Analysis
her kennen. Diese Entwicklungen gelten nur für ein bestimmtes Kreisgebiet
 um
um  herum,
herum,
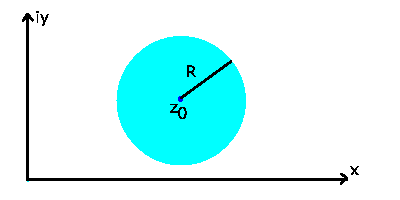
Abbildung 15:
Konvergenzgebiet der geometrischen Reihe.
Wenn  in
in  singulär ist, müssen in der Reihenentwicklung
auch Terme mit negativem Index
singulär ist, müssen in der Reihenentwicklung
auch Terme mit negativem Index 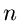 auftreten. Wir setzen allgemein
auftreten. Wir setzen allgemein
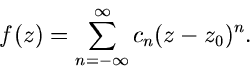 |
(56) |
Die Koeffizienten 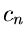 berechnet man am einfachsten, indem man beide
Seiten durch
berechnet man am einfachsten, indem man beide
Seiten durch
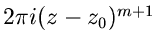 dividiert und ein Kreisintegral
auf einem Weg
dividiert und ein Kreisintegral
auf einem Weg 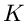 um
um  herum bildet,
herum bildet,
Mit Hilfe der Formeln (43) und (44) schließen wir,
und damit
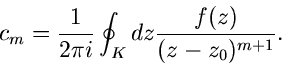 |
(57) |
Die möglichen Werte für die Koeffizienten können noch weiter
eingeschränkt werden. Hat  in
in  einen Pol der Ordnung
einen Pol der Ordnung 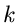 ,
so ist offensichtlich die Funktion
,
so ist offensichtlich die Funktion
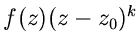 in
in  regulär, d.h. mit Hilfe der Formel (55)
regulär, d.h. mit Hilfe der Formel (55)
oder
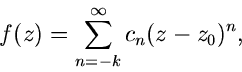 |
(58) |
d.h die Ordnung 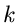 der Singularität gibt den negativen Startwert des
Summations- Index an. Entsprechend schließt man für eine
der Singularität gibt den negativen Startwert des
Summations- Index an. Entsprechend schließt man für eine 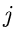 -fache
Nullstelle in
-fache
Nullstelle in  :
:
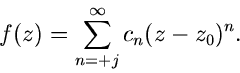 |
(59) |
Residuum.
Als Besonderheit der Laurent- Entwicklung bemerken wir, daß
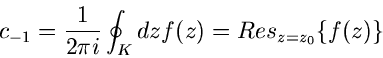 |
(60) |
ist, d.h. der erste negative Koeffizient der Reihenentwicklung um den
Punkt  ist gleich dem Kreisintegral der Funktion
ist gleich dem Kreisintegral der Funktion  um
um  .
Diesen Sachverhalt kann man ausnutzen, um Kreisintegrale zu berechnen.
Der Koeffizient
.
Diesen Sachverhalt kann man ausnutzen, um Kreisintegrale zu berechnen.
Der Koeffizient 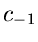 hat einen besonderen Namen, nämlich das Residuum
von
hat einen besonderen Namen, nämlich das Residuum
von  an der Stelle
an der Stelle  .
.
Besitzt  an der Stelle
an der Stelle 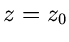 einen
einen 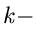 fachen Pol, dann kann das
Residuum an dieser Stelle mit der Formel
fachen Pol, dann kann das
Residuum an dieser Stelle mit der Formel
![\begin{displaymath}
c_{-1} = \frac{1}{2 \pi i} \oint_{K} dz f(z)
= \lim_{z \to...
...}} \frac{1}{(k-1)!} \left[ f(z) (z-z_{0})^{k}
\right]^{(k-1)}
\end{displaymath}](img215.gif) |
(61) |
berechnet werden. Der Index 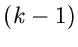 an der eckigen Klammer bedeutet wie
üblich eine
an der eckigen Klammer bedeutet wie
üblich eine 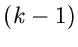 -fache Ableitung. Diese Formel folgt sofort aus
(58), was wir in der Form
-fache Ableitung. Diese Formel folgt sofort aus
(58), was wir in der Form
schreiben können.
Falls der Integrationsweg 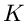 mehrere singuläre Stellen
mehrere singuläre Stellen
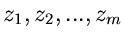 einschließt, mit den Ordnungen
einschließt, mit den Ordnungen
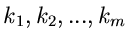 , so gilt nach Formel (51):
, so gilt nach Formel (51):
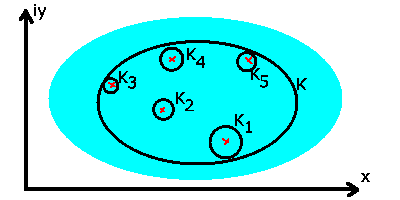
Abbildung 16:
Residuum von mehreren singulären Punkten.
Handelt es sich dabei ausschließlich um Pole 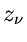 mit den Ordnungen
mit den Ordnungen
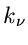 , so gilt die zu (61) verallgemeinerte Formel
, so gilt die zu (61) verallgemeinerte Formel
![\begin{displaymath}
c_{-1} = \frac{1}{2 \pi i} \oint_{K} dz f(z) = \sum_{\nu=1}^...
...)!} \left[ f(z) (z-z_{\nu})^{k_{\nu}}
\right]^{(k_{\nu} -1)} .
\end{displaymath}](img221.gif) |
(62) |
Beispiel.
Die Funktion
mit 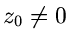 hat an der Stelle
hat an der Stelle 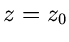 einen dreifachen und an der
Stelle
einen dreifachen und an der
Stelle 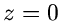 einen einfachen Pol. Die Grenzwerte sind
einen einfachen Pol. Die Grenzwerte sind
Die Kreisintegrale auf den Wegen 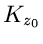 um
um  und
und 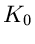 um
um
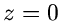 sind daher
sind daher
Das Kreisintegral auf dem Weg 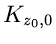 um beide Singularitäten
ergibt
um beide Singularitäten
ergibt
Beispiel.
Die Funktion
mit
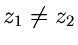 hat je einen einfachen Pol in
hat je einen einfachen Pol in 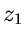 und
und 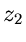 .
Die Residuen in den beiden Polen sind
.
Die Residuen in den beiden Polen sind
Das Kreisintegral auf einem Weg
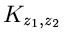 um beide Singularitäten
ist daher
um beide Singularitäten
ist daher
Beispiel.
Die Integration mittels der Residuenformel kann ausgenutzt werden, um
Integrale auf der reellen Achse zu berechnen. Wir wollen dieses Verfahren
an einem Beispiel erläutern. Die Funktion
besitzt je einen einfachen Pol bei
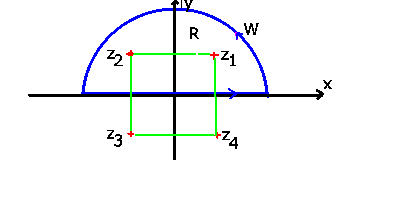
Abbildung 17:
Pole der im Text behandelten rationalen Funktion.
Wir wählen einen Integrationsweg 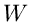 um die beiden Pole
um die beiden Pole 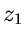 und
und 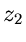 .
Dieser Weg
.
Dieser Weg 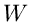 besteht aus einem Halbkreis
besteht aus einem Halbkreis 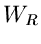 mit Radius
mit Radius 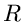 und
einem Weg
und
einem Weg 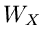 längs der Reellen Achse. Mit Hilfe der Residuenformel
erhalten wir
längs der Reellen Achse. Mit Hilfe der Residuenformel
erhalten wir
oder, da
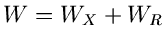 ,
,
Da  eine 4-fache Nullstelle im Unendlichen besitzt , verschwindet
offensichtlich das Integral über den Halbkreis für
eine 4-fache Nullstelle im Unendlichen besitzt , verschwindet
offensichtlich das Integral über den Halbkreis für 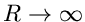 .
In demselben Maße wie das Integral auf
.
In demselben Maße wie das Integral auf  kleiner wird für
wachsendes
kleiner wird für
wachsendes  , vergrößert sich der Wert des Integrals auf der reellen
Achse. Im Grenzfall gilt offensichtlich
, vergrößert sich der Wert des Integrals auf der reellen
Achse. Im Grenzfall gilt offensichtlich
oder
Schlussbemerkung
Damit wollen wir die Behandlung der komplexen Funktionen beenden. Wenn Sie alles verstanden haben,
wissen Sie etwas mehr, als im Folgenden benötigt wird. Schaden kann das allemal nicht. Die Theorie
der komplexen Funktionen (Funktionentheorie) ist nach meinem Geschmack eines der interessantesten
Gebiete der Mathematik.
Harm Fesefeldt
2006-04-03
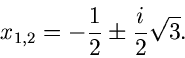

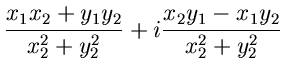
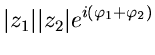
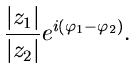
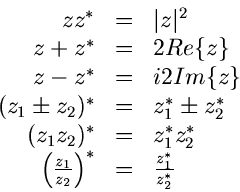
![]() mit zum Gebiet zählt oder nicht. Mathematisch exakter
ausgedrückt sagt man, ein Gebiet ist beschränkt, wenn sich eine (reelle)
Zahl
mit zum Gebiet zählt oder nicht. Mathematisch exakter
ausgedrückt sagt man, ein Gebiet ist beschränkt, wenn sich eine (reelle)
Zahl ![]() angeben läßt, sodaß
angeben läßt, sodaß

![]() - bzw
- bzw ![]() - Achse, werden durch
- Achse, werden durch
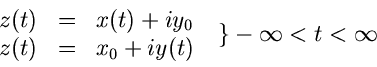
![]() - Wert
ein bestimmter
- Wert
ein bestimmter ![]() - Wert zugeordnet wird,
- Wert zugeordnet wird, ![]() , so definiert man im
Komplexen eine Zuordnung einer komplexen
, so definiert man im
Komplexen eine Zuordnung einer komplexen ![]() - Ebene auf eine komplexe
- Ebene auf eine komplexe
![]() - Ebene. Jedem Punkt
- Ebene. Jedem Punkt ![]() wird durch
wird durch ![]() eine Zahl
eine Zahl ![]() zugeordnet (siehe Abb.3).
zugeordnet (siehe Abb.3).

![]() im Punkte
im Punkte ![]() wird ähnlich wie im Reellen durch die Existenz der Grenzwerte
wird ähnlich wie im Reellen durch die Existenz der Grenzwerte
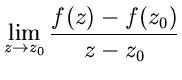
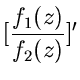
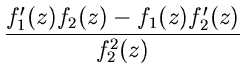
![]() nach
nach ![]() existieren und
identisch gleich sein. Diese Forderung führt zu einer starken
Verschärfung des Differentiationsbegriffes in der komplexen Ebene
verglichen mit der auf der reellen Zahlengeraden. Wir diskutieren die
Grenzwerte auf zwei Wegen, nämlich Weg I parallel zur reellen Achse
und Weg II parallel zur imaginären Achse (siehe Abb.4).
existieren und
identisch gleich sein. Diese Forderung führt zu einer starken
Verschärfung des Differentiationsbegriffes in der komplexen Ebene
verglichen mit der auf der reellen Zahlengeraden. Wir diskutieren die
Grenzwerte auf zwei Wegen, nämlich Weg I parallel zur reellen Achse
und Weg II parallel zur imaginären Achse (siehe Abb.4).

![]() und somit
und somit
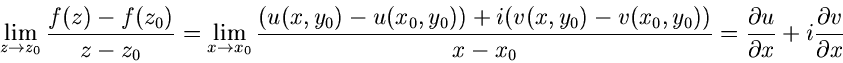
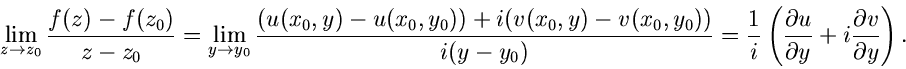
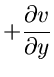
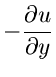
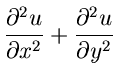
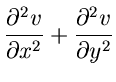
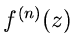 . Daher sind die Laplaceschen Differentialgleichungen
weitere notwendige Bedingungen, die
. Daher sind die Laplaceschen Differentialgleichungen
weitere notwendige Bedingungen, die 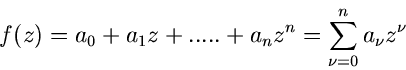
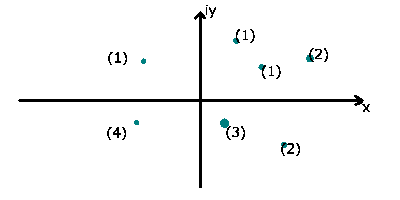
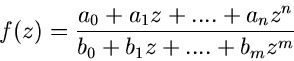
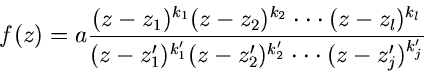

![]() des Nennerpolynoms
gleich einer Nullstelle
des Nennerpolynoms
gleich einer Nullstelle ![]() des Zählerpolynoms ist. In diesem Fall
entspricht das Verhalten der Funktion
des Zählerpolynoms ist. In diesem Fall
entspricht das Verhalten der Funktion ![]() für
für ![]() dem der
Funktion
dem der
Funktion
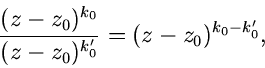
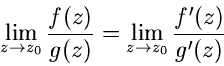
![]() im Unendlichen.
Der Funktion
im Unendlichen.
Der Funktion ![]() wird für
wird für ![]() das Verhalten zugeordnet,
daß die Funktion
das Verhalten zugeordnet,
daß die Funktion
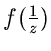 für
für ![]() zeigt. Danach können
ganze rationale Funktionen wie auch gebrochene rationale Funktionen im
Unendlichen regulär sein, einen mehrfachen Pol oder eine mehrfache
Nullstelle besitzen.
zeigt. Danach können
ganze rationale Funktionen wie auch gebrochene rationale Funktionen im
Unendlichen regulär sein, einen mehrfachen Pol oder eine mehrfache
Nullstelle besitzen.
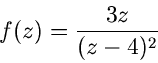
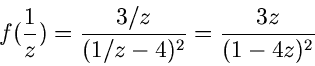
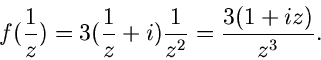
![]() führt zur
Potenzfunktion,
führt zur
Potenzfunktion,
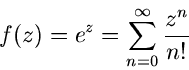
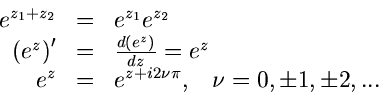
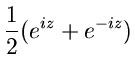
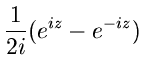
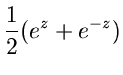
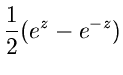
![]() in der komplexen Ebene, dargestellt in der
Parameterform
in der komplexen Ebene, dargestellt in der
Parameterform

![]() längs des Weges
längs des Weges ![]() ist dann definiert als
ist dann definiert als
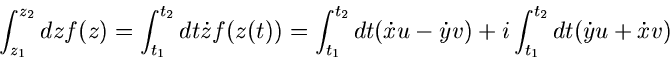
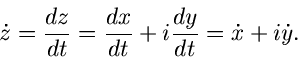
![]() - Ebene auf zwei reelle Integrale
zurückgeführt wurde, gelten formal die gleichen Regeln wie im Reellen:
- Ebene auf zwei reelle Integrale
zurückgeführt wurde, gelten formal die gleichen Regeln wie im Reellen:
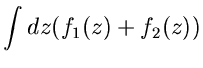
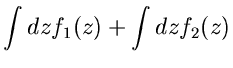
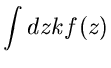
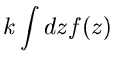
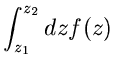
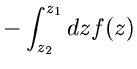
![]() und dem Mittelpunkt
und dem Mittelpunkt
![]() (der Parameter
(der Parameter ![]() ist durch
ist durch
![]() ersetzt),
ersetzt),
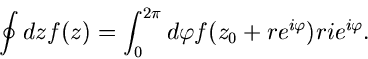

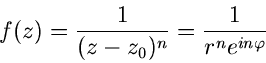
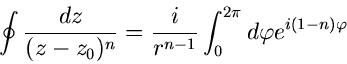
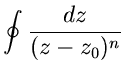
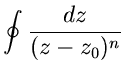
![]() in einem einfach zusammenhängenden Gebiet G regulär,
dann ist
in einem einfach zusammenhängenden Gebiet G regulär,
dann ist
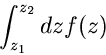
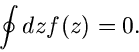

![]() , die in einem Gebiet
, die in einem Gebiet ![]() regulär ist.
Die Funktion
regulär ist.
Die Funktion
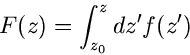
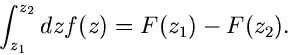
![]() regulär
ist. In dem unschraffierten Bereich braucht
regulär
ist. In dem unschraffierten Bereich braucht ![]() nicht regulär zu sein,
es können dort singuläre Stellen liegen (Abb.10).
nicht regulär zu sein,
es können dort singuläre Stellen liegen (Abb.10).

![]() und
und ![]() können wir zunächst nichts aussagen, da das Gebiet G nicht einfach
zusammenhängend ist, wir den Hauptsatz also nicht anwenden können.
Wir können
können wir zunächst nichts aussagen, da das Gebiet G nicht einfach
zusammenhängend ist, wir den Hauptsatz also nicht anwenden können.
Wir können ![]() und
und ![]() aber in zwei andere Kurven
aber in zwei andere Kurven ![]() und
und ![]() zerlegen, wie in der folgenden Skizze dargestellt (Abb.11).
zerlegen, wie in der folgenden Skizze dargestellt (Abb.11).

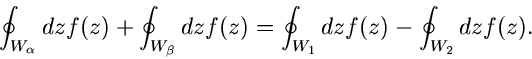
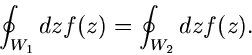

![]() möge
möge ![]() singuläre Bereiche (Stellen) einschließen,
dann gilt:
singuläre Bereiche (Stellen) einschließen,
dann gilt:
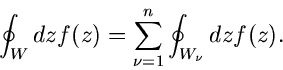
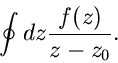

![]() um den Mittelpunkt
um den Mittelpunkt
![]() ,
,
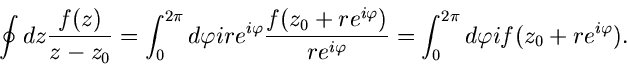
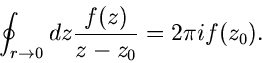
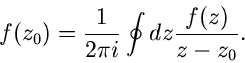
![]() eine
bis auf endlich viele singuläre Stellen
eine
bis auf endlich viele singuläre Stellen
![]() reguläre Funktion. Sei
reguläre Funktion. Sei ![]() insbesondere im Unendlichen für
insbesondere im Unendlichen für
![]() regulär. Wir bilden das Integral
regulär. Wir bilden das Integral
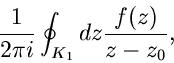

![]() möge darüber hinaus auch noch
möge darüber hinaus auch noch
![]() einschließen. Wir schneiden das Ringgebiet in gewohnter Weise
auf und bilden das Integral auf dem von
einschließen. Wir schneiden das Ringgebiet in gewohnter Weise
auf und bilden das Integral auf dem von ![]() ,
, ![]() und den beiden
Verbindungslinien gebildeten Weges
und den beiden
Verbindungslinien gebildeten Weges ![]() . Für diesen Weg kann die Formel
(52) angewendet werden, da
. Für diesen Weg kann die Formel
(52) angewendet werden, da ![]() jetzt innerhalb des geschlossenen
Weges
jetzt innerhalb des geschlossenen
Weges ![]() liegt, und
liegt, und ![]() in diesem Gebiet regulär ist.
in diesem Gebiet regulär ist.
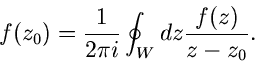
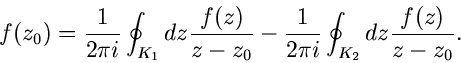
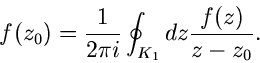
![]() -malige Differentiation liefert
-malige Differentiation liefert
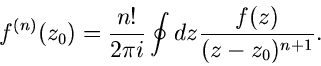
![]() herum. Wenn die Funktion
herum. Wenn die Funktion ![]() in
in ![]() regulär ist, gilt
die Reihenentwicklung
regulär ist, gilt
die Reihenentwicklung
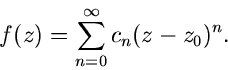

![]() in
in ![]() singulär ist, müssen in der Reihenentwicklung
auch Terme mit negativem Index
singulär ist, müssen in der Reihenentwicklung
auch Terme mit negativem Index ![]() auftreten. Wir setzen allgemein
auftreten. Wir setzen allgemein
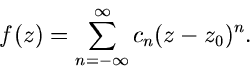
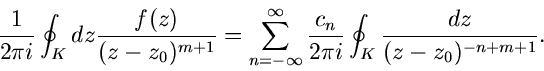
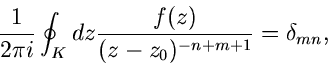
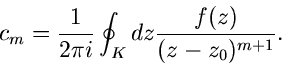
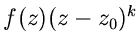 in
in 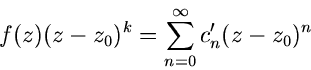
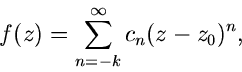
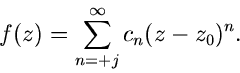
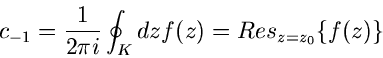
![]() an der Stelle
an der Stelle ![]() einen
einen ![]() fachen Pol, dann kann das
Residuum an dieser Stelle mit der Formel
fachen Pol, dann kann das
Residuum an dieser Stelle mit der Formel
![\begin{displaymath}
c_{-1} = \frac{1}{2 \pi i} \oint_{K} dz f(z)
= \lim_{z \to...
...}} \frac{1}{(k-1)!} \left[ f(z) (z-z_{0})^{k}
\right]^{(k-1)}
\end{displaymath}](img215.gif)
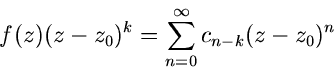
![]() mehrere singuläre Stellen
mehrere singuläre Stellen
![]() einschließt, mit den Ordnungen
einschließt, mit den Ordnungen
![]() , so gilt nach Formel (51):
, so gilt nach Formel (51):
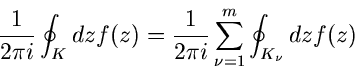

![]() mit den Ordnungen
mit den Ordnungen
![]() , so gilt die zu (61) verallgemeinerte Formel
, so gilt die zu (61) verallgemeinerte Formel
![\begin{displaymath}
c_{-1} = \frac{1}{2 \pi i} \oint_{K} dz f(z) = \sum_{\nu=1}^...
...)!} \left[ f(z) (z-z_{\nu})^{k_{\nu}}
\right]^{(k_{\nu} -1)} .
\end{displaymath}](img221.gif)
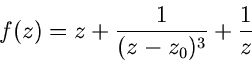
![$\displaystyle \frac{1}{2!} \lim_{z \to z_{0}} [ f(z) (z-z_{0})^{3}]^{(2)}$](img225.gif)
![$\displaystyle \lim_{z \to 0} [ f(z) z ]^{(0)}$](img227.gif)
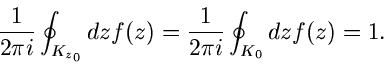
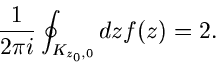
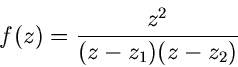
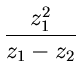
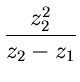
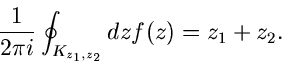
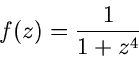
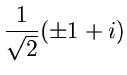
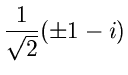

![]() um die beiden Pole
um die beiden Pole ![]() und
und ![]() .
Dieser Weg
.
Dieser Weg ![]() besteht aus einem Halbkreis
besteht aus einem Halbkreis ![]() mit Radius
mit Radius ![]() und
einem Weg
und
einem Weg ![]() längs der Reellen Achse. Mit Hilfe der Residuenformel
erhalten wir
längs der Reellen Achse. Mit Hilfe der Residuenformel
erhalten wir