Im Zahlenlotte ,,6 aus 49'' werden nacheinander 6 Kugeln aus einem Behälter
mit 49 durchnumerierten Kugeln gezogen. Hierbei muß man bei der Definition
des Elementarereignisses aufpassen. Es wäre falsch anzunehmen, daß
das einmalige Ziehen einer Kugel ein Elementarereignis wäre und das
Ereignis A= ,,6 aus 49'' dann aus 6 Elementarereignissen gebildet
werden könnte. Dieser Ansatz wäre nur dann korrekt, wenn jede Kugel
nach dem Ziehen wieder in den Behälter zurückgelegt
und durch Mischen der Kugeln der gleiche Bedingungskomplex wie beim
ersten Zug wiederhergestellt werden würde. Wenn die Kugel dagegen
nicht zurückgelegt wird, wie es beim Zahlenlotto auch tatsächlich der Fall
ist, hat man bei jedem folgenden Zug jeweils eine Kugel weniger im
Behälter und damit einen veränderten Bedingungskomplex.
Elementarereignisse können aber nur für ein und denselben
Bedingungskomplex definiert werden. Der einzig richtige Ansatz ist in
diesem Versuch, das sechsmalige Ziehen einer Kugel als Elementarereignis
zu definieren. Auf die Reihenfolge der gezogenen Zahlen kommt es hierbei
nicht an. Die Zahlen werden am Ende der Ziehung in aufsteigender
Reihenfolge sortiert.
Die Anzahl der Elementarereignisse findet man mit Hilfe
der Kombinatorik (siehe später in diesem Abschnitt) zu
In diesem Beispiel und in fast allen Anwendungen der Statistik kann man die Anzahl und Definition der Elementarereignisse mit Hilfe der 4 Grundaufgaben der Kombinatorik lösen. Im folgenden werden wir die 4 Grundaufgaben angeben und durch Beispiele erläutern. Für Beweise verweisen wir auf die einschlägige Literatur.
1.Grundaufgabe
Es seien n voneinander verschiedene Elemente gegeben. In wieviel
verschiedenen Anordnungen (Permutationen) kann man dieselben in eine
Reihe nebeneinander stellen, oder wenigstens gestellt denken?
Satz: Die Anzahl der Permutationen von n verschiedenen Elementen
ist gleich dem Produkt
| (1) |
Ein typisches Beispiel ist die Gruppenaufnahme. Ein Fotograf soll n verschiedene Personen, die in einer Reihe stehen, fotografieren. Die Personen können sich nicht einigen, wer neben wem steht. Der Fotograf macht daher den Vorschlag, Aufnahmen von allen nur denkbaren Anordnungen zu machen. Jeder kann sich dann hinterher die ihm genehme Anordnung aussuchen. Dieser Fotograf hat seinen Vorschlag ohne Kenntnis der Kombinatorik gemacht. Wie man aus Formel (1) ersieht, würde sein Film mit 24 Bildern bei einer Familie mit 4 Personen gerade noch ausreichen. Dagegen müßte er bei einer Fußballmanschaft praktisch schon die gesamte Jahresproduktion der deutschen Filmindustrie aufkaufen.
Eine Permutation stellt man mathematisch dadurch da, daß man die geänderte
Reihe unter die originale Reihe schreibt, z.B.
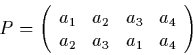
2.Grundaufgabe
Es seien n Elemente gegeben, welche nicht alle voneinander verschieden
sind, sondern so in p Arten,
![]() , zerfallen, daß die
Elemente jeder einzelnen Art einander gleich, jedoch Elemente
verschiedener Art verschieden sind. Die erste dieser Arten enthalte
, zerfallen, daß die
Elemente jeder einzelnen Art einander gleich, jedoch Elemente
verschiedener Art verschieden sind. Die erste dieser Arten enthalte
![]() , die zweite
, die zweite ![]() , ..., die letzte
, ..., die letzte ![]() Elemente.
Wie groß ist unter diesen Voraussetzungen die Anzahl der
Permutationen?
Elemente.
Wie groß ist unter diesen Voraussetzungen die Anzahl der
Permutationen?
Satz: Die Anzahl der Permutationen in der 2. Grundaufgabe der
Kombinatorik ist durch
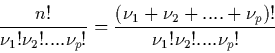 |
(2) |
Wir greifen noch einmal das Beispiel der 1. Grundaufgabe auf, verändern es aber dahingehend, daß die Gruppe aus m Männern und f Frauen besteht. Die Männer und Frauen untereinander haben sich bereits darauf geeinigt, sich der Größe nach aufzustellen. Zwischen den Männern untereinander und den Frauen untereinander braucht der Fotograf also nicht mehr zu unterscheiden. Falls es sich hierbei um die Bonner Bundesregierung mit 12 männlichen und 3 weiblichen Ministern handeln sollte, hätte der Fotograf die Wahl zwischen 455 verschiedenen Möglichkeiten.
3.Grundaufgabe
Wenn n Elemente gegeben sind und k eine natürliche, nicht oberhalb n
gelegene Zahl bezeichnet, so nennt man jede Zusammenstellung, die man
erhält, wenn man irgendwelche k der gegebenen Elemente herausgreift und
in irgendeine Anordnung nebeneinander stellt, eine Kombination
k-ter Ordnung der gegebenen Elemente. Wenn zwei Kombinationen,
welche die gleichen Elemente in verschiedener Anordnung enthalten, als
verschieden gelten sollen, so spricht man von Kombinationen mit
Berücksichtigung der Anordnung, sonst von Kombinationen ohne
Berücksichtigung der Anordnung. Sind die gegebenen Elemente
untereinander verschieden, sodaß auch in den von ihnen gebildeten
Kombinationen nur verschiedene Elemente auftreten, so spricht man
von Kombinationen ohne Widerholung (oder auch Variationen).
Man soll also, wenn n eine beliebige und k eine
nicht oberhalb von n gelegene natürliche Zahl bedeutet, die Anzahl der
Kombinationen k-ter Ordnung von n voneinander verschiedenen Elementen
ermitteln, und zwar 1.) mit Berücksichtigung der Anordnung und 2.)
ohne Berücksichtigung der Anordnung.
Satz: Unter den gemachten Voraussetzungen der 3. Grundaufgabe ist die
Anzahl der Kombinationen mit Berücksichtigung der Anordnung durch das
Produkt
| (3) |
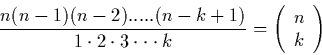 |
(4) |
Wir greifen noch einmal das Lottospiel ,,6 aus 49'' auf. Da die Reihenfolge
der Zahlen hierbei keine Rolle spielt, erhalten wir tatsächlich die bereits
oben angegebene Anzahl von Spielmöglichkeiten. Würde die Reihenfolge
eine Rolle spielen, so würde sich die Zahl der verschiedenen Spiele
auf
![]() erhöhen. Wir haben in diesem Beispiel stillschweigend
die sogenannte Zusatzzahl ausser acht gelassen. Bei der Ziehung der
Zusatzzahl spielt die Reihenfole eine Rolle, sie wird nämlich
tatsächlich als letzte Zahl gezogen. Dieses Beispiel wird in den
Aufgaben behandelt.
erhöhen. Wir haben in diesem Beispiel stillschweigend
die sogenannte Zusatzzahl ausser acht gelassen. Bei der Ziehung der
Zusatzzahl spielt die Reihenfole eine Rolle, sie wird nämlich
tatsächlich als letzte Zahl gezogen. Dieses Beispiel wird in den
Aufgaben behandelt.
4.Grundaufgabe
Es seien n Arten von Elementen gegeben, von denen jede mehrere, und zwar
wenigstens k Elemente enthält. Die Elemente jeder einzelnen Art seien
einander gleich, aber Elemente verschiedener Arten seien verschieden.
Dann ist es möglich, Kombinationen der gegebenen Elemente zu bilden,
in welchen mehrere gleiche Elemente vorkommen, und solange man nur solche
Kombinationen betrachtet, welche nicht mehr als k Elemente enthalten,
ist die Anzahl der gleichen Elemente, welche in ein und dieselbe
Kombination aufgenommen werden dürfen, einer Einschränkung nicht
unterworfen. Es sind also n verschiedene Elemente gegeben, aber bei der
Bildung von Kombinationen dieser Elemente zu je k darf jedes einzelne
Element unbeschränkt oft wiederholt werden. Dieses nennt man auch kurz
Kombination mit Wiederholung. Man kann sich diesen Sachverhalt
auch anschaulich folgendermaßen vorstellen. Ein Drucker hat 26
Kästen mit Buchstaben, für jeden Buchstaben einen Kasten. Er soll
Wörter mit k gleichen oder verschiedene Buchstaben schreiben,
wobei die Anzahl der Buchstaben in jedem Kasten mindestens gleich k
ist, damit die Bildung von Wörtern aus k gleichen Buchstaben
überhaupt möglich ist. Gefragt ist nach der möglichen Zahl der Wörter mit
k Buchstaben, die man erhält, wenn man es dem Zufall überläßt, aus
welchem Kasten man einen Buchstaben entnimmt. Hierbei sehen wir
natürlich jede Zusammenstellung von Buchstaben als ein Wort an.
Dieses führt uns zur 4. Grundaufgabe, die folgendermaßen formuliert
werden kann.
Man soll die Anzahl der Kombinationen k-ter Ordnung von n verschiedenen,
unbeschränkt oft wiederholbaren Elementen ermitteln, und zwar 1.)
mit Berücksichtigung der Anordnung und 2.) ohne Berücksichtigung
der Anordnung.
Satz: Die Anzahl der Kombinationen k-ter Ordnung von n verschiedenen,
unbeschränkt oft wiederholbaren Elementen ist gegeben durch
| (5) |
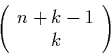 |
(6) |
Eine einfache Anwendung hierzu ist die folgende Aufgabe. Die Zeichen
des in der Telegrafie benutzten Morse Alphabets sind aus nur zwei
verschiedenen Elementen, Punkt und Strich, zusammengesetzt. Wieviel
Zeichen lassen sich aus diesen Elementen bilden, wenn zur Bildung eines
Zeichens nicht mehr als 5 Elemente verwendet werden dürfen. Die
Antwort ist einfach. Da es hierbei auf die Reihenfolge ankommt, erhalten wir
aus (5) mit n=2 und k= 1,2,3,4,5 die Lösung
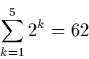
Rekursive Relationen
Häufig kommt man allerdings bei der Lösung
von kombinatorischen Problemen mit den 4 Grundaufgaben alleine nicht aus.
Dieses tritt im allgemeinen dann auf, wenn die Anordnungen der Elemente
weiteren Einschränkungen unterworfen wird. Ein Beispiel möge dieses
verdeutlichen. Gesucht ist die Anzahl ![]() der möglichen Dualzahlen
der möglichen Dualzahlen
![]() mit
mit ![]() Stellen. Eine Dualzahl mit
Stellen. Eine Dualzahl mit ![]() Stellen ist bekanntlich durch
eine Anordnung von
Stellen ist bekanntlich durch
eine Anordnung von ![]() Nullen und Einsen gegeben. Gemäß der 4. Grundaufgabe
(
Nullen und Einsen gegeben. Gemäß der 4. Grundaufgabe
(![]() ) ergeben sich
) ergeben sich ![]() verschiedene Zahlen. Führt man allerdings als
Nebenbedingung ein, daß niemals 2 Einsen nebeneinander stehen dürfen, so
wird die Anzahl der Möglichkeiten stark reduziert. Für
verschiedene Zahlen. Führt man allerdings als
Nebenbedingung ein, daß niemals 2 Einsen nebeneinander stehen dürfen, so
wird die Anzahl der Möglichkeiten stark reduziert. Für ![]() erfüllen die
Dualzahlen 0 und 1 die Bedingung, also ist
erfüllen die
Dualzahlen 0 und 1 die Bedingung, also ist ![]() . Für
. Für ![]() erfüllen
nur 00, 01 und 10 die Nebenbedingung, also
erfüllen
nur 00, 01 und 10 die Nebenbedingung, also ![]() . Entsprechend ist
. Entsprechend ist
![]() und
und ![]() . Der allgemeine Schluß von
. Der allgemeine Schluß von ![]() auf
auf ![]() geht
wie folgt. Wenn
geht
wie folgt. Wenn ![]() in der letzten Stelle eine Null hat, so sind auch
alle
in der letzten Stelle eine Null hat, so sind auch
alle ![]() Zahlenkombinationen in den vorhergehenden Stellen erlaubte
Kombinationen für
Zahlenkombinationen in den vorhergehenden Stellen erlaubte
Kombinationen für ![]() . Hat
. Hat ![]() umgekehrt in der letzten Stelle
eine Eins, so darf in der vorhergehenden Stelle keine Eins auftreten.
Erlaubte Kombinationen sind nur die
umgekehrt in der letzten Stelle
eine Eins, so darf in der vorhergehenden Stelle keine Eins auftreten.
Erlaubte Kombinationen sind nur die ![]() Kombinationen für die
Kombinationen für die ![]() Stellen der Dualzahl
Stellen der Dualzahl ![]() . Zusammengefaßt ergibt sich
. Zusammengefaßt ergibt sich