Der Ereignisraum

Kausale und zufällige Ereignisse
Alle Erscheinungen und Ereignisse in der uns umgebenden Welt sind voneinander abhängig und beeinflussen sich gegenseitig. Dabei ist jede beobachtete Erscheinung kausal durch eine meist sehr große Anzahl anderer Phenomene und Bedingungen ursächlich bestimmt. Wir nennen dieses den Bedingungskomplex $K$. Die Realisierung des Bedingungskomplexes heißt Versuch und das Versuchsergebnis nennen wir ein Ereignis. Nach dieser Definition gibt es eigentlich keine zufälligen Ereignisse. Trotzdem wird in der Statistik je nach Kompliziertheit des Bedingungskomplexes zwischen kausalen und zufälligen Ereignissen unterschieden. Ist der Bedingungskomplex relativ einfach und leicht überschaubar, sprechen wir von einem kausalen Ereignis. Ist umgekehrt der Bedingungskomplex zu kompliziert um mathematisch erfaßt zu werden, sprechen wir von einem zufälligen Ereignis.

Ein Beispiel möge diesen Sachverhalt verdeutlichen. Gegeben sei ein Widerstand $R$, an den wir eine Spannung $U$ anlegen (Realisierung des Bedingungskomplexes). Das Ergebnis dieses Versuches läßt sich leicht vorhersagen. Durch den Widerstand $R$ fließt ein Strom $I=U/R$. Der Bedingungskomplex ist hier besonders einfach, er besteht aus dem Widerstand $R$ und der Spannung $U$, das Ereignis ist der Strom $I$. Wir sprechen von einem kausalen Ereignis. Das Ergebnis dieses Versuches wird zu einem zufälligen Ereignis, wenn der Widerstand $R$ und die Spannung $U$ nicht genau bekannt sind, wenn z.B. unsere Meßapperatur zu schlecht ist, oder wenn der Widerstand $R$ und die Spannung $U$ zeitlich nicht konstant sind, z.B. durch Temperaturschwankungen oder Netzinstabilitäten. Der Bedingungskomplex ist zu kompliziert geworden, um eine sichere Vorhersage zu gewährleisten. Ob ein Versuch kausale oder zufällige Ereignisse liefert, hängt also entscheidend vom Bedingungskomplex ab.

In vielen Fällen ist also der Bedingungskomplex so kompliziert oder gar nicht vollständig bekannt, sodaß wir nicht in der Lage sind, das Ereignis mit Sicherheit vorherzusagen. Wir sprechen dann von zufälligen Ereignissen. Das klassische Beispiel hierfür ist der Spielwürfel mit völlig homogener und symmetrischer Beschaffenheit. Beim Würfeln läßt sich nicht vorhersagen, welche Augenzahl nach dem Wurf oben liegt. Der zu dem Versuch gehörige Bedingungskomplex $K$ ist außerordentlich kompliziert. Er hängt von der Bewegungsform der den Würfel führenden Hand, von der Beschaffenheit der Oberflächen von Würfel und Tisch u.s.w. ab. Wir definieren daher folgendermaßen.
Der Unterschied zwischen einem kausalen und einem zufälligen Ereignis besteht darin, daß beim kausalen Ereignis der den Versuch beschreibende Bedingungskomplex $K$ vollständig angebbar und mathematisch beschreibbar ist, während beim zufälligen Ereignis die Bedingungen des Komplexes unvollständig, nicht genau bekannt sind oder in ihrer Gesamtheit mathematisch nicht erfaßt werden können.
Wenn wir im folgenden von Ereignis sprechen, meinen wir immer ein zufälliges Ereignis.

Elementarereignis
Der Begriff des Elementarereignisses ist ein Grundbegriff der Wahrscheinlichkeitsrechnung. Wir definieren:
Kann ein zufälliges Ereignis nur auf eine Weise und mit keinem anderen Ereignis zusammen eintreffen, so heißt es Elementarereignis.
Wir bezeichnen Elementarereignisse mit $E$. Wir erläutern diesen Begriff durch das Würfelspiel. Die Elementarereignisse sind hier durch das Würfeln einer der Zahlen von 1 bis 6 gegeben, wir haben also 6 Elementarereignisse. Das Würfeln einer bestimmten Zahl schließt das Würfeln einer anderen Zahl als Ergebnis des Versuches aus. Weitere Ereignisse sind z.B.:

$$\begin{array}{l} X_{1} = \; Augenzahl \; ist \; gerade \\ X... ...eq \; 1 \\ X_{5} = \; Augenzahl \; ist \; > \; 1. \end{array}$$

In diesen Beispielen ist offenbar $X_{2}$ identisch mit dem Elementarereignis $E_{6}$, also $X_{2}=E_{6}$. Alle anderen Beispiele dagegen sind keine Elementarereignisse. $X_{1}$ ist z.B. erfüllt, wenn $E_{2}$, $E_{4}$ oder $E_{6}$ eintreten. $X_{1}$ kann zusammen mit allen anderen Ereignissen $X_{2}$ bis $X_{5}$ eintreffen. $X_{4}$ und $X_{5}$ sind offensichtlich identische Ereignisse. Dieses führt uns auf eine Schwierigkeit der Wahrscheinlichkeitsrechnung. Ereignisse können identisch sein, obwohl sie mathematisch und sprachlich völlig verschieden sind. Entscheidend ist nur, ob beide Ereignisse dieselben Elementarereignisse enthalten, was z.B. bei $X_{4}$ und $X_{5}$ der Fall ist, nämlich $E_{2}$ bis $E_{6}$.

Die Anzahl der Elementarereignisse hängt entscheidend von der Versuchsanordnung ab. Wenn unsere Augen so schlecht wären, daß wir die Anzahl der Punkte auf den Würfeln nicht genau erkennen könnten, sondern nur die Ergebnisse ,,Augenzahl $\leq$ 3'' und ,,Augenzahl $>$ 3'' auf Grund des Schwärzungsgrades ausmachen könnten, hätten wir nur 2 Elementarereignisse.

Ereignisraum
Es ergibt sich also folgende Situation. Gegeben ist ein gewisser Bedingungskomplex $K$ (Versuch), dem wir eine bestimmte Anzahl von Elementarereignissen $E_{1}$, $E_{2}$,...., $E_{n}$ zuordnen können. Die Gesamtheit der Elementarereignisse $E_{\nu}$ $(\nu= 1,2,...,n)$, die bei der Realisierung des Bedingungskomplexes eintreten können, bilden den Ereignisraum $I$. Jedem Einzelproblem der Wahrscheinlichkeitsrechnung muß also ein abstraktes System von Elementarereignissen zugeordnet werden. Man kann den Ereignisraum geometrisch darstellen durch ein Schachbrett- artiges Muster (siehe Abb.1), in dem jedes Feld ein Elementarereignis darstellt. Ein beliebiges Ereignis $X$ wird dann durch eine Fläche im Ereignisraum $I$ dargestellt. Exaktere mathematische Formulierungen werden später angegeben.

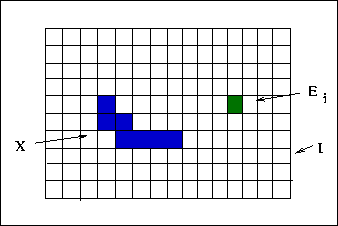
Abbildung 1: Geometrische Darstellung des Ereignisraumes.

Klassifizierung
Wir unterscheiden die Ereignisräume nach der Anzahl der in ihnen enthaltenen Elementarereignisse $E_{\nu}$. Endliche Ereignisräume enthalten nur endlich viele Elementarereignisse:

$$I = (E_{1},E_{2},.....,E_{n}).$$ (1)

Enthält der Ereignisraum abzählbar viele Elementarereignisse, läßt sich also jedem Elementarereignis eine wenn auch beliebig große Zahl $n$ zuordnen,

$$I = (E_{1},E_{2},..........),$$ (2)

so spricht man von einem abzählbar unendlichen Ereignisraum. Ein überabzählbarer Ereignisraum

$$X= (E_{i}, i \in N),$$ (3)

ist gegeben, wenn die Indexmenge $N$ sich nicht mehr durchnumerieren läßt, wenn z.B. $N=R$ die Menge aller reellen Zahlen ist.

Ereignis als Teilmenge.
Wir haben im vorhergehenden (siehe auch Abb.1) schon angedeutet, was wir unter einem Ereignis verstehen wollen. Wir werden dieses jetzt präziser formulieren. Gegeben sei ein endlicher Ereignisraum $I=(E_{1},E_{2},...E_{n})$. Wir definieren:
1. Jede Teilmenge $X=(E_{i_{1}},E_{i_{2}},....,E_{i_{k}})$ mit $1 \leq k \leq n$ des Ereignisraumes $I$ ist ein zufälliges Ereignis in $I$.
2. Das zufällige Ereignis $X$ ist eingetreten, wenn das auftretende Elementarereignis $E_{\nu}$ ein Element dieser Teilmenge $X$ ist.
Wir können diese Definitionen formelmäßig schreiben als

$$X \subset I, \; \; wenn \; E_{\nu} \in X.$$ (4)

Man muß hier also klar unterscheiden. Der Versuch liefert eines und nur eines der Elementarereignisse $E_{\nu}$, ein beliebiges Ereignis kann sich aber aus mehreren Elementarereignissen zusammensetzen. Insbesondere können zwei oder mehrere zufällige Ereignisse auch miteinander vereinbar sein, d.h. sie können auch zugleich auftreten. Allerdings darf es sich dann nicht um Elementarereignisse handeln. Diese Situation ist noch einmal in Abb.2 skizziert. Die die Ereignisse darstellenden Flächen überschneiden sich und die Ereignisse können daher gemeinsam auftreten.

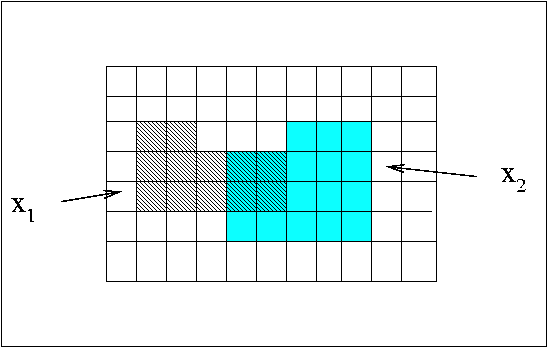
Abbildung 2: Illustration zum Begriff des Ereignisses.

Im Falle unseres Spielwürfels können die beiden Ereignisse

$$\begin{array}{l} X_{1} = \; Augenzahl \; ist \; gerade \\ X_{3} = \; Augenzahl \; ist \; durch \; 3 \; teilbar \end{array}$$

gemeinsam auftreten, nämlich genau dann, wenn die Augenzahl 6 gewürfelt wird.

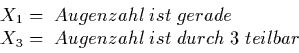
Menge Z der zufälligen Ereignisse
Nach obiger Definition ist jede Teilmenge $X=(E_{i_{1}},E_{i_{2}},...,E_{i_{k}})$ aus $I$ ein zufälliges Ereignis in $I$. Die Elementarereignisse $E_{i}$ sind selbst natürlich auch zufällige Ereignisse in $I$. Wir nehmen noch zwei Grenzfälle hinzu. Der eine tritt auf, wenn das Ereignis $X$ alle Elementarereignisse umfaßt, $X=(E_{1},E_{2},...,E_{n})$. Dieses ist offenbar ein sicheres Ereignis des Versuches und daher ein kausales Ereignis. In diesem Fall ist $X=I$. Weiterhin nehmen wir das unmögliche Ereignis hinzu und bezeichnen es mit 0. Es wird durch die Teilmenge in $I$ repräsentiert, die kein Elementarereignis enthält, also durch die leere Menge.

Für einen Ereignisraum mit 3 Elementarereignissen, also $I=(E_{1},E_{2},E_{3})$ ergibt sich die Menge $Z$ der zufälligen Ereignisse zu

$$\begin{array}{ll} 3 \; Elementarereignisse & (E_{1}), (E_{2}... ...{2},E_{3}) \\ 1 \; unm''ogliches \; Ereignis & 0. \end{array}$$

Wir erhalten also $8=2^{3}$ zufällige Ereignisse. Dieses Ergebnis kann man durch Induktion leicht verallgemeinern zu:
Bei einem Ereignisraum $I$ mit $n$ Elementarereignissen enthält die Menge $Z$ der zufälligen Ereignisse $2^{n}$ Elemente, von denen allerdings nur $2^{n}-1$ wirklich auftreten können.
Wir haben hier eine etwas lässige Schreibweise benutzt. Was wir mit $(E_{i},E_{j})$ meinen, ist die logische ODER Verknüpfung $E_{i}+E_{j}$. Logische Verknüpfungen zwischen Ereignissen werden später noch ausführlich diskutiert.

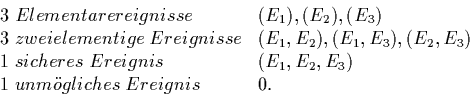
Pseudozufallszahlen
In jeder Programmiersprache gibt es einen Pseudozufallszahlen- Generator. Diese Systemroutine liefert bei aufeinanderfolgenden Aufrufen eine Gleichverteilung von Zahlen in einem gewissen Intervall [a,b]. Die Zahlen werden im Sinne der vorhergehenden Erläuterungen als unabhängig angenommen, d.h. eine in einem bestimmten Funktionsaufruf gelieferte Zahl hängt nicht von den vorherigen Aufrufen ab. Wie weit diese Unabhängigkeit bei den Zufallszahlen- Generatoren wirklich gewährleistet ist, wird in einem späteren Kapitel noch einmal ausführlich diskutiert. Wir werden dann sehen, daß genau das Gegenteil der Fall ist. Jeder Zufallszahlen- Generator erzeugt Zahlen nach einem bestimmten Algorithmus. Jede folgende Zahl wird aus der vorhergehenden Zufallszahl berechnet. Warum man trotzdem so tun kann als ob die Zahlen unabhängig wären, muß dann ausführlich diskutiert werden. Im folgenden werden wir davon ausgehen, daß der Generator Zufallszahlen im Intervall [0,1] liefert.

Wir haben soeben immer einen Begriff benutzt, der uns in diesem Tutorial noch häufig begegnen wird, nämlich den Begriff des Generators. Unter einem Generator verstehen wir allgemein eine Programm- Routine, die Zufallszahlen mit einem bestimmten Verteilungsgesetz berechnet. Wir prüfen die Annahme der Gleichverteilung des Zufallszahlen- Generators der Java Sprache im folgenden Applet. Wir haben hier einen Spielwürfel programmiert. Durch Ziehen mit der Maus kann man den Würfel rotieren, durch einmaliges Doppelklicken irgendwo in das Appletfenster wird eine Zufallsrotation ausgeführt. Mit Hilfe zweier Zoom- Buttons kann der Würfel verkleinert oder vergrößert werden. Die Ergebisse des Würfelns können in einem Histogramm gesammelt werden. Dazu müssen Sie den Knopf Show Plot anklicken und dafür sorgen, daß alle Fenster gleichzeitig auf Ihrem Bildschirm sichtbar sind. Mein Ergebnis nach 100 Würfen ist in Abb.3 gezeigt. Oben rechts im Histogramm- Fenster sind noch die Anzahl der Versuche (Entries), die Anzahl der ausserhalb des Koordinatenbereiches liegenden Ereignisse (Overflow, Underflow), sowie Mittelwert und Streuung (Average, Sigma) der Verteilung Die beiden letzteren Begriffe werden in einem späteren Kapitel ausführlich diskutiert. Durch Drücken des Buttons ChangePlot kann das Histogramm gelöscht werden.

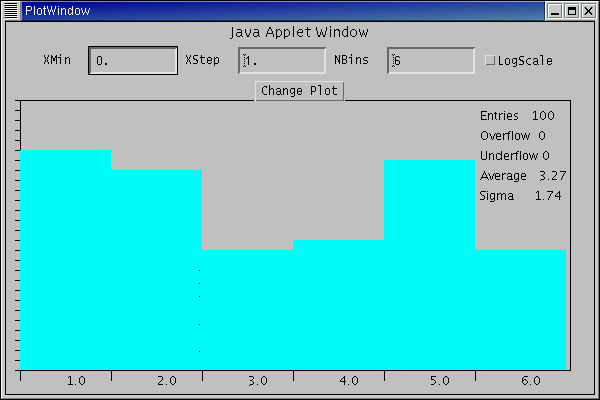
Abbildung 3: Gleichverteilung in einer Simulation mit dem Zufallszahlen- Generator der Java Programmiersprache.

Der einmalige Aufruf des Zufallszahlen- Generators ist in unserem Sinne ein Versuch. Alle Zahlen im Intervall [0,1] bilden ein System von Elementarereignissen,

$$E_{j} = \{ x_{j}, x_{j} \in [0,1] \}.$$

Da die Anzahl der Nachkommastellen in jedem Digitalrechner beschränkt ist, handelt es sich un einen endlichen Ereignisraum mit endlich vielen Elementarereignissen. Gleichverteilung der Zahlen bedeutet, daß die Wahrscheinlichkeit $P(E_{j})=1/n$ für jedes Elementarereignis gleich groß ist. n ist hierbei natürlich eine beliebig große Zahl. Wir können den Ereignisraum des Zufallszahlen- Generators verkleinern, indem das Zahlenintervall [0,1] in m gleich große Intervalle aufgeteilt wird und die Elementarereignisse $E_{j}'$ durch

$$E_{j}' = \{ x, x\in [\frac{j-1}{m},\frac{j}{m}] \}, \; j=1,2,...,m$$

definiert werden. Vergrößern dagegen kann man den Ereignisraum des Zufallszahlen- Generators nicht.

Zusammenfassung
Ein experimenteller Versuch, der durch einen Bedingungskomplex $K$ beschrieben wird, liefert als Ergebnis zufällige Ereignisse. Die Grundaufgabe der Statistik besteht darin, eine Menge von Elementarereignissen zu finden, die sich gemäß Definition gegenseitig ausschließen. Die Zuordnung der zunächst nur sprachlich formulierten Elementarereignisse zu einem abstrakten Schema $I=(E_{1},E_{2},...,E_{n})$ ist die Grundaufgabe jeder statistischen Analyse. Ein beliebiges Ereignis $X$ des Versuches kann dann in einer noch exakter zu formulierenden Weise durch die Elementarereignisse ausgedrückt werden. Die Gesamtzahl der Ereignisse in einem Ereignisraum mit $n$ Elementarereignissen beträgt $2^{n}$, von denen allerdings nur $2^{n}-1$ auftreten können.
Übungen
Aufgabe 1:
Der endliche Ereignisraum $I$ bestehe aus den 4 Elementarereignissen $E_{1}$, $E_{2}$, $E_{3}$ und $E_{4}$. Geben Sie sämtliche zufälligen Ereignisse an.
Aufgabe 2:
a) Wieviele zufällige Ereignisse gibt es beim Würfeln mit zwei verschiedenfarbigen Würfeln ?
b) Im folgenden Applet. wird die Summe der Augenzahlen zweier Würfel gezählt. Bei welchem Wert erwarten Sie das Maximum der Verteilung ?
Aufgabe 3:
a) Ein Würfelspiel bestehe aus 3 gleichen Würfeln. Sie dürfen bis zu dreimal würfeln, jedoch müssen Sie nach jedem Wurf mindestens einen Würfel beiseite legen. Gezählt wird am Ende nur die Summe der Augenzahlen der drei Würfel. Wieviele Elementarereignisse gibt es bei diesem Spiel ?
b) In Abänderung zur Aufgabe Teil a) können Sie im folgenden Applet. nach jedem Wurf jeden Würfel aus dem Spiel herausnehmen oder wieder in das Spiel hineinbringen. Sie deaktivieren den Würfel, indem Sie ein wenig mit der Maus an dem Würfel ziehen, bis er in Graustufen dargestellt wird. Mit dem Reset-Button können Sie alle Würfel wieder in das Spiel zurückbringen. Wenn alle Würfel deaktiviert sind, spätestens aber nach dem dritten Wurf, wird das Ergebnis in den Plot eingetragen und die nächtse Spielrunde beginnt. Entwickeln Sie eine Strategie, um eine möglichst hohe Punktzahl zu erreichen.