
We will explore three basic numbering systems, called decimal,
binary, and hexadecimal.
A base 10 number system, the decimal system, is based on ten
numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The next number in the
sequence is a combination of two digits, where the second digit is multiplied
by 10. 10 is equal to (1 X 10) + 0. Two digits may
go as high as 99, and then a third digit is needed for the next number.
The third digit is multiplied by 100. This concept continues with
the next digit multiplied by 1000, the next by 10,000, and
so on. A number like 6594 would be calculated as (6 X 1000) +
(5 X 100) + (9 X 10) + (4 X 1). This concept is easy to grasp, because
we use the decimal system in every day applications.
 |
Computers work in a digital environment that has only two variables,
0 and 1. All numbers in the decimal system may be translated
into 0's and 1's of the binary system. By having only one
digit or box, there are two possibilities. This binary system
is a base 2 numbering system that uses only two numbers, 0 and 1. |
|
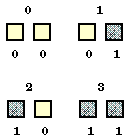
| By having two digits or boxes, there are four possibilities.
The upper number is the decimal counting system and the bottom numbers represent
the binary counting system. In binary, the first digit (right box) corresponds
to a decimal value of 0 or 1, while the second digit (left box) corresponds
to a decimal value of 0 or 2. The multiples of the decimal counting system
are 1, 10, 100, 1000, etc. The multiples of the binary counting system are
1, 2, 4, 8, 16, 32, 64, 128, etc. |
 |
|
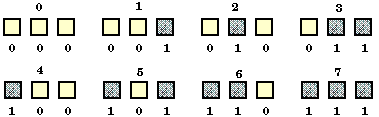
| By having three digits or boxes, there are eight possibilities.
The upper number is the decimal counting system and the bottom numbers represent
the binary counting system. The first digit (right box) may have a value
of 0 or 1. The second digit (middle box) may have a value of 2 or 0 and
the last digit (left box) may have a value of 4 or 0. |
 |
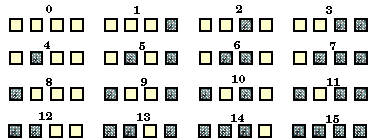 |
By having four digits or boxes, there are sixteen possibilities. |
| (Remember that 0 is a number, 0-15) The upper number is the decimal counting
system and the boxes represent the binary possibilities. |
| This is the same diagram, but now you only see the binary representation. |
 |
| The first digit (right box) may have a value of 0 or 1, and the second
digit may have a value of 2 or 0, the third digit may have a value of 4
or 0, and the last digit (left box) may have a value of 8 or 0. |
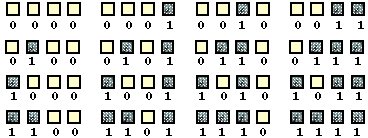
| Finally, we see all the combinations, with the upper numbers representing
the decimal counting system followed by the [hexadecimal counting
system]. The bottom number is the binary equivalent of the upper
numbers. |
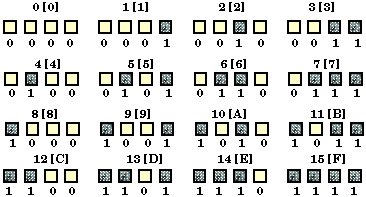 |
The hexadecimal counting system is a base 16 system.
Each digit or slot may be represented by sixteen possible numbers. Hexadecimal
uses the first ten numbers of the decimal system: 0, 1, 2, 3, 4, 5, 6,
7, 8, and 9. The number 10 has two digits so in hexadecimal
it is represented by the letter A. The number 11, by B,
12 by C, 13 by D, 14 by E and
15 by F.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14,
15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22, 23, 24, 25, 26,
27, 28, 29, 2A ........etc.
Two digits or slots are needed to represent the next number in the sequence.
The decimal number 16 would equal 10 in hexadecimal. (1
X 16) + 0. Continuing in the series, 17(decimal) would equal
11(hexadecimal), 18(decimal) would equal 12(hexadecimal),
and so on until 31(decimal), which would equal 1F(hexadecimal).
The next hexadecimal number would be 20, (2 X 16) + 0, which
would equal 32 in decimal. The hexadecimal number 9C would
equal (9 X 16) + 12 = 156 in decimal.
| multiple of each digit |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
| binary counting system |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
The binary number 10110110 is the equivalent of 182
in decimal. That is, (128 x 1) + (64 x 0) + (32 x 1) + (16 x 1) +
(8x0) + (4 x 1) + (2 x 1) + (1 x 0).
| multiple of each digit |
256 |
16 |
1 |
| hexadecimal counting system |
1 |
A |
F |
The hexadecimal number 1AF is the equivalent of 321
in decimal. That is (256 x 1) + (16 x 10) + (1 x 15). The multiples
of the digits in the hexadecimal counting system are 1, 16, 256, etc.
So why do we have to learn all these numbers to understand MIDI?
Remember that MIDI digital information is transmitted using the binary
system. The serial interface translates musical actions or events into binary
numbers that it receives and sends one at a time down a MIDI cable. By understanding
the binary counting system, we can look at MIDI information and understand
what is being transmitted through a MIDI cable. The binary number 10010000
is not easy to calculate, but reading the number in the hexadecimal equivalent
90 makes more sense when it is applied to a MIDI message.
10010000, 00110111, 01111011 = 90, 37, 7B, which may be interpreted
as;
Note ON, MIDI channel 1, play the 55th note, at a velocity of 123 out of
127 possibilities.
| multiple of each digit |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
| binary counting system |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
If we look at the binary number above there is an easier way to add up
the number. Instead of counting the binary number as (128 x 1) + (64
x 0) + (32 x 1) + (16 x 1) + (8x0) + (4 x 1) + (2 x 1) + (1 x 0) =
182 (Decimal), split the binary number into two sections.
| multiple of each digit |
8 |
4 |
2 |
1 |
|
8 |
4 |
2 |
1 |
| binary counting system |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
0 |
| hexadecimal counting system |
B |
|
|
|
|
6 |
|
|
|
(8 X 1) + (4 X 0) + (2 X 1) + (1 X 1) = 11 or B in hexadecimal
(8 X 0) + (4 X 1) + (2 X 1) + (1 X 0) = 6 in hexadecimal
B6 hexadecimal number (11[B] x 16) + 6 = 182 in decimal
If we use eight binary digits we have 256 possible numbers. 00000000
to 11111111. We can use two hexadecimal numbers to represent 256
numbers, 00 to FF. All MIDI events may be represented with
eight binary or two hexadecimal numbers.
You may download a document,Conversion of Numbers,
that was created using the program Max. This document compares the similarities
between the decimal, binary and hexadecimal counting systems.By clicking
on the document your browser should download the file. The document may
be changed back to its original version by using the program StuffIt Expander.
If your browser is set up to recognize StuffIt Expander, it may have already
unstuffed the document. If not, you will need to obtain a copy of the program
StuffIt Expander from Aladdin.
The program MAXplay is needed to run the document Conversion of Numbers.
If you would like information about the application Max, please contact
Opcode Systems, Inc.. You may download
a free copy of this application by clicking on the MAXplay icon below. This
is a run-time only version of the application Max; it may not be used to
create new Max documents. MAXplay will work only on a Macintosh computer.
 Conversion of Numbers(MAXplay document) (17k)
Conversion of Numbers(MAXplay document) (17k)
 MAXplay 3.0 (Application) (644k)
MAXplay 3.0 (Application) (644k)
 |
|
|
|
Understanding Decimal Binary & Hexadecimal
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|






