

Sometimes, this subject is a little confusing because both formats are referred to as digital information. This page will try to explain the content of both signals and clear up some misconceptions about the two formats.
First let us start by describing an analog signal. The word analog implies
a resemblance or similar comparison of one thing representing another. An
analog signal is a transformation of an acoustic signal, movement of molecules
in a medium such as air, to a voltage signal that travels down an electrical
wire. The voltage in the wire is an analog or representation of the acoustic
signal. A typical set-up may be a musical instrument that creates a tone.
This tone energy creates a disturbance in the air particles by pushing air
molecules that condense and cause a rarefaction of the air when it returns.
This movement is happening at a fast rate that equals the initial source
of the soundwave. This tone is then received by a microphone that has a
sensitive diaphragm that responds to the movement of air. At this point
we use a term called transducer, because the energy is converted from an
acoustic signal to an electrical signal than represents the same waveform.
This voltage signal is then carried down a wire to an amplifier, where the
signal is amplified and then sent down another wire to a loudspeaker, which
transforms the signal back to acoustic energy that is received by the auditory
system.
Another example of analog signals are the use of the older modular type
synthesizers that use voltage to carry the musical signal down a wire. Alterations
to the signal, such as filters, ring modulators, simple frequency modulation,
sample and hold are modifiers that are used to alter the analog signal.
In the digital world, numbers are used to represent a digital waveform.
An audio signal is represented in digital memory with a binary code that
stores a massive amount of numbers that are used to represent a signal.
An ADC (Analog to Digital Converter) is a computer chip that is used
to convert an analog signal into digital information. This process is called
sampling and has changed the world of sound in a dramatic fashion.
Once the signal is represented as binary numbers, it may be manipulated
with processes like combining sounds, splicing, truncation, looping, and
reversing a sound and other digital signal processing. The signal is then
converted back to an analog signal through a DAC (Digital to Analog Converter).
In order to sample a sound event we must understand the process that is
used to convert the acoustic waveform to a digital sample.
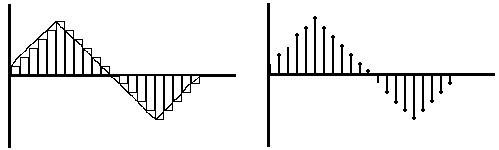
The user has to determine the sampling period or rate and must also decide
on the bit resolution. Let's use a time period of one second for a sample.
During that second of time, the sampling rate determines the number of samples
that will be taken during that one second. The bit resolution determines
where to represent the signal during that discrete moment in time. If the
resolution is at 16 bits, then there would be 32, 768 locations
to represent the waveform at each given sample. That would be a range from
-16384 to 0 to 16383. If the resolution is 8 bits, there would be
256 possible locations. The term quantizing is when the actual
sample is shifted to one of the bit locations that best represents the signal
at that discrete moment in time. If we changed the sampling rate,
the period of time or space between each sample is changed. In the diagram
below are four examples of different quantization and sampling rates.
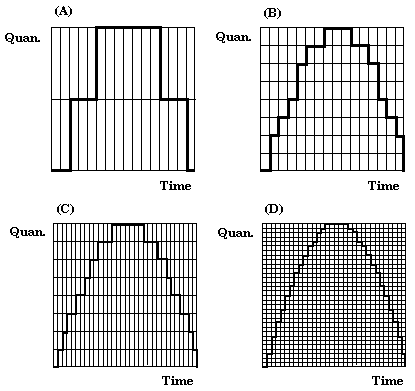 |
In diagram (A) and (B) the sampling rate is the same, but the quantization
resolution is better in diagram (B). In diagram (C) & (D), the sampling
rate has been doubled and the bit resolution has been increased in diagram
(D). What a dramatic difference the sampling rate and bit resolution can
make on recreating an acoustic waveform.
The Nyquist Theorem determines that the bandwidth of any digital
sampling length will always be one-half of the sampling rate. This means
that a sample taken at a rate of 44k would have 22k (22,000) pictures or
snap shots of the waveform in one second of time. A higher rate will have
more samples per second and will also take up more computer memory. The
Nyquist Frequency is the frequency of the highest component of a
sound and the Nyquist Rate is twice the Nyquist Frequency.
More computer memory is also used when the bit resolution is higher (16
bits to represent a number verses 8 bits). Computer memory and the content
that is being sampled will determine the sampling rate and bit resolution
to use. For example, sounds that do not have a high frequency content could
be sampled at a lower rate and still imitate most of the same fidelity as
the original sound.
It is important that the signal that is being sampled does not have frequencies
above the Nyquist Frequency. Every time that a sample is made, there is
also duplicates of the signal that are also created that are called Folding
Components.
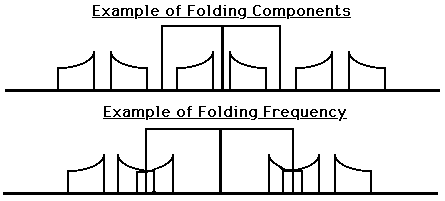
When a sample goes beyond the sampling rate, the duplicate of the signal
crosses over into the sampling range and is considered the Folding Frequency.
We use the term aliasing to describe the folding frequencies which
are doubles of the frequencies. In the sampling process filters are used
before the ADC to make sure that the folding frequency will not happen when
the signal is sampled.
| In digital sampling, the number of bits per sample also determines the signal to noise ratio. The signal to noise ratio depends on how loud the signal is. The following ratio is used to determine the decibel ratio. |
|
 |
Clearly, digital sampling is a very complicated concept and in order to truly capture an acoustic waveform, a quality sample will need a large amount of computer memory. Use the following formula to get a better idea of how large the file size is of a sampled audio sound. |
| (# seconds) * (# channels) * (sampling rate) * (bit resolution) / 8 = file size |
Take the number of seconds and times it by the number of channels (mono
or stereo). Times that by the sampling rate and the bit resolution. Then
divide the total by eight to get the file size.
Example 1- Sampling a four second sound of a speaking voice.
Because the voice is in the lower range of the audio spectrum we could sample
the sound at 11kHz with one mono channel and 8 bit resolution.
Example 2 - Sampling a four second sound of a musical selection.
First we need to change the sampling rate to 44kHZ to capture the spectrum
of the complex musical sound and we will record a stereo sample with 16
bit resolution.
Both examples are four seconds of sound, but the final output is very
different in size (44k vs. 704k). If we tried to take example 2 and
record a minutes worth of sound, the sound file would expand to 10,560k
or 10.6megabytes, while a minutes worth of sound from example
1 would be 660k. Both examples are one minute long, but the difference
in the size of the files is 9900k or 9.9 megabytes.
![]() Return to Audio vs. MIDI
Menu
Return to Audio vs. MIDI
Menu
It is important to understand that MIDI contains performance data or instructions for creating music. The actual analog audio signal or digital audio signal, are not moving through a MIDI cable.
The type of performance data that is communicated by MIDI includes:
If we look at the hexadecimal and binary code of a MIDI file, we will discover
that the amount of information is drastically reduced in comparison with
a digital audio file. A one second digital audio file may be around 700k,
while a one second MIDI file might contain 1 to 3k of information.
With MIDI we are not recording or sampling the actual note. Instead, we
are sending information to turn on a MIDI devices sound. Go to the MIDI Language for more detail.
![]() Return to Audio vs. MIDI
Menu
Return to Audio vs. MIDI
Menu